Question

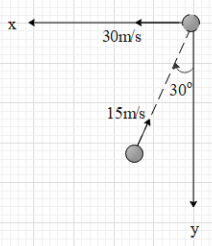
A hockey player receives a corner shot a speed of $15m{{s}^{-1}}$ at angle ${{30}^{\circ }}$ with y-axis and then shoots the ball along x-axis with the speed $30m{{s}^{-1}}$, if the mass of the ball is 150g and it remains in contact with the hockey stick for 0.01s, the force exerted on the ball along x-axis is:

A. 281 N
B. 187.5 N
C. 562.5 N
D. 375 N

Answer 1

Hint:Force is defined as the change momentum of a body power time. Calculate the initial and final momentums of the ball along the x-axis. Then calculate the change in momentum of the ball along the x-axis. Later, divide the change in momentum by the time for which the ball is in contact.

Formula used:
$F=\dfrac{\Delta P}{t}$,
where F is the applied force on the body for time t, $\Delta P$ is the change in momentum of the body.
$P=mu$,
where P is the momentum of a body of mass m and moving with velocity u.

Complete step by step answer:
Force is defined as the change in momentum of a body power time. If the momentum of a body changes by $\Delta P$ in time t, then the force applied on it for time t is given as $F=\dfrac{\Delta P}{t}$
$F=\dfrac{\Delta P}{t}$ ….. (i)
It is sad that we are supposed to find the force exerted on the ball along the x-axis.
Let us find the initial momentum of the ball along the x-axis. It is given that the mass of the ball is $m=150g=0.15kg$ and its initial velocity is$15m{{s}^{-1}}$. We can see in the figure that this velocity makes an angle of ${{60}^{\circ }}$ with the x-axis. Therefore, the initial velocity of the ball along x-axis is,
${{u}_{x}}=15\cos {{60}^{\circ }}\\
\Rightarrow{{u}_{x}} =15\times \dfrac{1}{2}\\
\Rightarrow{{u}_{x}} =7.5m{{s}^{-1}}$.
But we see that the velocity is along the negative x-axis.
${{u}_{x}}=-7.5m{{s}^{-1}}$
This means that initial momentum of the ball along x-axis is,
${{P}_{i}}=m{{u}_{x}}\\
\Rightarrow{{P}_{i}} =(0.15)(-7.5)\\
\Rightarrow{{P}_{i}} =-1.125kgm{{s}^{-1}}$.
It is said that the ball is in contact with the stick for a time $t=0.01s$. This means that force is exerted for a time $t=0.01s$. Then the ball travels with the velocity of ${{v}_{x}}=30m{{s}^{-1}}$ along the positive x-axis.
This means that the final momentum of the ball is,
${{P}_{f}}=m{{v}_{x}}\\
\Rightarrow{{P}_{f}} =(0.15)(30)\\
\Rightarrow{{P}_{f}} =4.5kgm{{s}^{-1}}$.
Therefore, the change in the momentum of the ball along x-axis is,
$\Delta P={{P}_{f}}-{{P}_{i}}\\
\Rightarrow\Delta P =4.5-(-1.125)\\
\Rightarrow\Delta P =5.625kgm{{s}^{-1}}$
Then the force exerted on the ball along x-axis is equal to
$F=\dfrac{\Delta P}{t}\\
\Rightarrow F =\dfrac{5.625}{0.01}\\
\therefore F =562.5N$.

Hence, the correct option is C.

Note:The change is momentum of a body is defined to be impulse produced in the body. From the equation (i), we can write that the impulse in the body is equal to $\Delta P=Ft$. This means that impulse produced in a body is equal to the product of force applied on it and the time for which the force is applied.