Question

A high-impedance ac voltmeter is connected in turn across the inductor, the capacitor, and the resistance in a series circuit having an ac source of 100V(rms) and gives the same reading in volts in each case. Then, this reading is:
A. $100/3\;{\rm{volts}}$
B. $300\;{\rm{volts}}$
C. $100\;{\rm{volts}}$
D. Incomplete data

Answer 1

Hint: For RLC circuits in series, consider the same current owing through the circuit and out the voltages across the inductor, capacitor and resistor. Apply the condition of resonance to and the value of the phase difference in the voltage and current. Then apply it in the power factor formula.

Formula used: The condition for resonance in an RLC series circuit:
${{\rm{X}}_{\rm{C}}}\; = \;{{\rm{X}}_{\rm{L}}}$

Complete step-by-step answer:
Given that the ac voltmeter is connected with capacitor, inductor and resistance in a series circuit having 100V(rms). The voltage across the resistor remains in phase with the current in the circuit. The voltage across the inductor leads the current by$\dfrac{\pi }{2}$.Whereas; the voltage across the capacitor lags the current by$\dfrac{\pi }{2}$. Since the components are connected in series, the same current flows through all the elements. Therefore, the following phasor diagram can be drawn.
Therefore ${{\rm{V}}_{\rm{C}}} = {{\rm{V}}_{\rm{L}}} = \;{{\rm{V}}_{\rm{R}}}\; = 100\;{\rm{V}}$ (given)

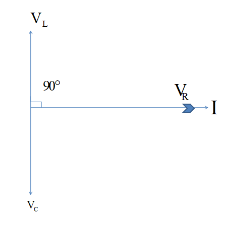
We know ${{\rm{V}}_{\rm{C}}} = \;{{\rm{X}}_{{\rm{C }}}}$ $ \Rightarrow {{\rm{X}}_{\rm{C}}} = \,100$
Also, ${{\rm{V}}_{\rm{L}}} = \;{{\rm{X}}_{\rm{L}}} = \;100$
Now from above resonance condition;
${{\rm{X}}_{\rm{C}}} = {{\rm{X}}_{\rm{L}}}$
$ \Rightarrow \;{{\rm{X}}_{\rm{C}}}{\rm{ - }}{{\rm{X}}_{\rm{L}}} = 0$
$\therefore {{\rm{V}}_{\rm{R}}} = {\rm{V = 100V}}$
It is a condition of resonance then the only potential on each is equal and 100V.

Hence the correct option is (C).

Note: At resonance in a circuit, the frequency of the source helps to balance the reactive elements in the circuit. The capacitive and the inductive load balance each other out. And the resultant impedance is only resistive. Thus, all the work done is the real work. Hence, by the definition of power factor, it becomes 1.