Question

A hemispherical bowl of radius unity is filled up with water up to depth $\dfrac{1}{2}$. The volume of water in the bowl is
$
  {\text{A}}{\text{. }}\dfrac{{27\pi }}{{24}} \\
  {\text{B}}{\text{. }}\dfrac{{5\pi }}{{24}} \\
  {\text{C}}{\text{. }}\dfrac{{3\pi }}{4} \\
  {\text{D}}{\text{. None of these}} \\
$

Answer 1

Hint: To start solving such questions, drawing a figure and naming it appropriately makes it simpler. Observing the figures in the diagram, apply Pythagoras theorem to find the radius of the hemisphere which is further used to compute the volume.

Complete step-by-step answer:
Given Data
Radius = 1, depth = $\dfrac{1}{2}$
According to the given question, our figure looks like this

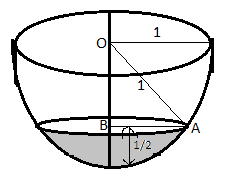
According to Triangle OAB from the figure,
OA (radius) =1 and OB (depth) = $\dfrac{1}{2}$
We know for a right angled triangle whose sides are a, b, c respectively
${{\text{a}}^2} + {{\text{b}}^{^2}} = {{\text{c}}^2}$ (Pythagoras theorem)
From figure side ${\text{AB = }}\sqrt {{\text{O}}{{\text{A}}^2} - {\text{O}}{{\text{B}}^2}} = \sqrt {1 - \dfrac{1}{4}} = \dfrac{{\sqrt 3 }}{2}$
Volume of a Hemisphere = $\dfrac{{2\pi }}{3}{{\text{r}}^3}$
To find the volume of water, we should determine the volume of the shaded hemisphere i.e.
V = $\dfrac{{\pi {\text{h}}}}{6}\left( {3{{\text{a}}^2} + {{\text{h}}^2}} \right)$
$
  {\text{Here a = AB = }}\dfrac{{\sqrt 3 }}{2},{\text{ h = }}\dfrac{1}{2} \\
   \Rightarrow {\text{V = }}\dfrac{\pi }{6} \times \dfrac{1}{2}\left[ {3{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{1}{2}} \right)}^2}} \right]{\text{ = }}\dfrac{{5\pi }}{4} \\
$
Hence Option B is the correct answer.

Note: To answer this type of question, drawing an accurate figure is the key. Then using the given data apply appropriate trigonometric equalities to find out the radius of the hemisphere we want to work on. Then with the help of the figure identify the portion of figure for which volume has to be calculated. On substituting the appropriate values in the formula, the required answer is determined.