Question

A hemispherical bowl of internal diameter 36 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 3 cm and height 9 cm. How many bottles are required to empty the bowl?
(a) 24
(b) 35
(c) 12
(d) 48

Answer 1

Hint: We will calculate the quantity of the liquid in the hemispherical bowl. For this, we will use the formula for the volume of the hemisphere which is given by ${{V}_{H}}=\dfrac{2}{3}\pi {{r}^{3}}$ where $r$ is the radius of the hemisphere. After that we will find the capacity of the cylindrical bottle. We will use the formula for the volume of the cylinder which is ${{V}_{C}}=\pi {{r}^{2}}h$, where $r$ is the radius of the cylinder and $h$, is its height. We will divide the volume of the liquid by the volume of the bottle to find the number of bottles required.

Complete step by step answer:
We have a hemispherical bowl of the internal diameter of 36 cm is full of liquid. Therefore, the inner radius of the hemispherical bowl is 18 cm.

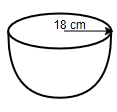
We can calculate the volume of the liquid by using the formula for the volume of a hemisphere. The volume of hemisphere is given by ${{V}_{H}}=\dfrac{2}{3}\pi {{r}^{3}}$ where $r$ is the radius of the hemisphere. Substituting $r=18$ in this formula we get,
$\begin{align}
  & \text{volume of liquid}=\dfrac{2}{3}\pi {{\left( 18 \right)}^{3}} \\
 & \Rightarrow \text{volume of liquid}=\dfrac{2}{3}\times \pi \times 5832 \\
 & \therefore \text{volume of liquid}=3888\pi \text{ c}{{\text{m}}^{3}} \\
\end{align}$
We have cylindrical bottles each of radius 3 cm and height 9 cm.

Now we will calculate the volume of the cylindrical bottle. For this, we will use the formula for the volume of cylinder which is ${{V}_{C}}=\pi {{r}^{2}}h$ where $r$ is the radius of the cylinder and $h$ is its height. Substituting $r=3$ and $h=9$ in this formula, we get the following
$\begin{align}
  & \text{volume of one bottle}=\pi \times {{\left( 3 \right)}^{2}}\times 9 \\
 & \therefore \text{volume of one bottle}=81\pi \text{ c}{{\text{m}}^{3}} \\
\end{align}$
Now, the number of bottles required to empty the bowl is
$\text{number of bottles}=\dfrac{\text{volume of liquid}}{\text{volume of one bottle}}$
Substituting the volume of liquid and the volume of one bottle in the above expression, we get
$\begin{align}
  & \text{number of bottles}=\dfrac{3888\pi }{81\pi } \\
 & \therefore \text{number of bottles}=48 \\
\end{align}$
Hence, 48 cylindrical bottles are required to empty the hemispherical bowl.
Therefore, the correct option is (d).

Note:
 It is important to understand the standard geometric shapes and the formulae for their volumes and areas. These formulae are useful in such type of questions. It is beneficial to do the calculations explicitly so that we can avoid making any errors and obtain the correct answer. The key aspect in this question is to understand that we have to distribute the total volume of liquid into cylindrical bottles and hence, we can find the number of bottles needed by dividing the volume of liquid by the volume of one such bottle.