Question

A heavy round log is suspended at the ends on two ropes so that the distance between the points of suspension of the ropes is equal to the diameter of the log. The length of each vertical segment of the ropes is $l$. Determine the period $T$ of small oscillations of the system in a vertical plane perpendicular to the log.

Answer 1

Hint:Oscillation is the periodic change of a measure around a central value (often a point of equilibrium) or between two or more states, usually in time. Mechanical oscillation is precisely described by the term vibration. Oscillation can be seen in a swinging pendulum and alternating current.

Complete step by step answer:

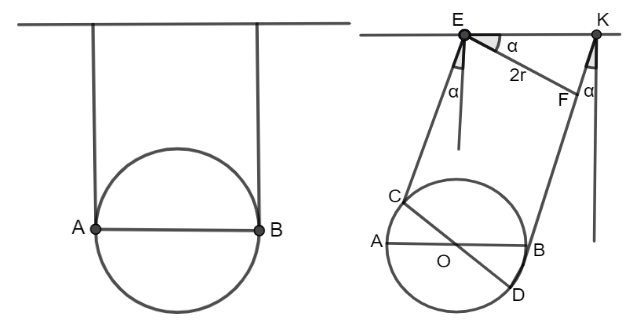
Let's make a note of the log's horizontal diameter AB = 2r when it passes through the equilibrium location. Consider the log at the moment when the ropes on which it is suspended are bent by a tiny angle from vertical\[{\text{ }}\alpha \].

We may simply find from geometrical considerations that the diameter AB always remains horizontal in the process of oscillations in the absence of rope slip.
Indeed,
if $EF \bot DK$
$FK = 2r\,\tan \alpha \approx 2r\alpha $
$BD \approx \dfrac{{FK}}{2} \approx r\alpha $
Consequently, $\angle BOD,\,\alpha $as was indicated above. Because the diameter AB remains horizontal at all times, the log moves in a translatory manner, which means that the velocities of all of its points are the same at all times. As a result, the log's motion is synchronised with the oscillation of a basic I-length pendulum. As a result, the period of minor log oscillations is,
$T = 2\pi \sqrt {\dfrac{l}{g}} $

Note:Let us see some more examples of oscillations. The beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, and geothermal oscillations are all examples of oscillations.