Question

A heavy but uniform rope of length L is suspended from a ceiling. A particle is dropped from the ceiling at the instant when the bottom end is given the jerk. Where will the particle meet the pulse
A. A. At a distance \[\dfrac{2L}{3}\] from the bottom.
B. At a distance \[\dfrac{L}{3}\] from the bottom.
C. At a distance \[\dfrac{3L}{4}\] from the bottom.
D. None of these

Answer 1

Hint: First we assume a length of rope that can act as a single mass system after that find the velocity in terms of mass and displacement and then we integrate the length with respect to the time given, for both the length assumed and for the whole rope separately. After getting the time for the wave to travel the rope, we use that time to find the place where the particle and wave on the rope meets. To find the time taken for the wave to travel in the rope, we use:
\[V=\sqrt{\dfrac{T}{m}}\]
And place the value of velocity V as \[\dfrac{dx}{dt}\] here T is the tension of the rope due to the mass system assumed on the rope and m is the mass of the rope’s mass system.

Complete step by step answer:
Let us draw a diagram as shown below and take any particular point on the rope from the bottom as \[dx\] and the length from the bottom to the \[dx\] as \[x\].

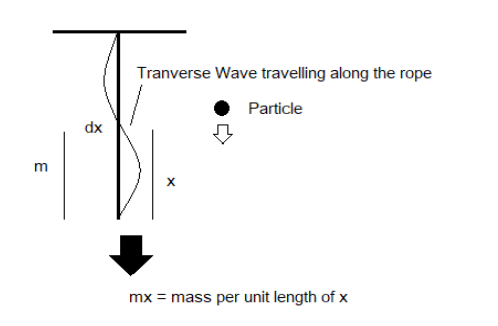
After this we take the mass per unit length of the rope as m.
Now the part from \[dx\] to bottom is taken as a single individual and is acting like a singular mass object and is suspended by the rest half of the rope, which is producing tension on the rope.
Hence, the tension of the rope is given as:
\[T\text{ }=\text{ }mg\]
Now the mass m here is the portion of the rope from bottom to \[dx\] and the mass per unit length of the portion is m thereby, making the mass of that \[x\] length potion as mx. With mass as \[mx\], we get the tension as:
\[T\text{ }=\text{ }mx\times g\]
Using the formula of the transverse wave velocity or speed of a wave on a spring as:
\[V=\text{ }\sqrt{\dfrac{T}{m}}\]
Replacing the value of the T in form of mass and gravity as shown above and placing the values in the velocity formula, we get the velocity of the wave in the string as:
\[V\text{ }=\text{ }\sqrt{\dfrac{mx\times g}{m}}\]
\[\Rightarrow V\text{ }=\text{ }\sqrt{xg}\]
Now we get the velocity in terms of distance.
After this we find the velocity with which the wave will move from bottom to top, using the integral method we find the time as shown below:
\[\dfrac{dx}{dt}\text{ }=\text{ }\sqrt{xg}\]
Shifting the dt part from RHS to LHS we get the integrating part as:
\[\int\limits_{0}^{T}{dt}=\int\limits_{0}^{L}{\dfrac{dx}{\sqrt{xg}}}\]
Integrating the LHS and RHS, we get the value of the time when the wave travels in L length of the rope.
\[t-0=\sqrt{\dfrac{4L}{g}}\]
Now, we take the distance left after we eliminate the length L and taking the length which was x as y and the distance of the rope above y as \[L\text{ }-\text{ }y\] and let us take the point where the particle and wave in the rope meet is at y distance from the bottom. Therefore, in this case the time by the wave travel when jerked and meeting the particle at y is given as
\[t\text{ }=\text{ }\sqrt{\dfrac{4y}{g}}\]
Now after the rope, the distance travelled by the particle and the meeting of the wave of the rope is given by the distance formula of the one-dimension kinematics:
\[S=ut+\dfrac{1}{2}g{{t}^{2}}\]
Placing the value of time t, in terms of y, and S as L we get the value of the y as:
\[\Rightarrow S=u\left( \sqrt{\dfrac{4y}{g}} \right)+\dfrac{1}{2}g{{\left( \sqrt{\dfrac{4y}{g}} \right)}^{2}}\]
\[\Rightarrow L=\dfrac{1}{2}g{{\left( \sqrt{\dfrac{4y}{g}} \right)}^{2}}\]
\[\Rightarrow L=3y\]
\[\therefore y=\dfrac{L}{3}\]

Therefore, the particle and the wave on the rope meet at \[y=\dfrac{L}{3}\].

Note:
Students may go wrong while calculating the time taken by the particle separately although if the velocity of the particle is given or found out then we can equate it with the wave velocity of the rope but as the velocity of the particle is not given. Hence, we will find the velocity of the wave on the rope until a certain distance and equate it with the wave velocity of the whole rope as the wave velocity until a certain distance is the same as that of the velocity of the particle moving from ceiling to bottom.