Question

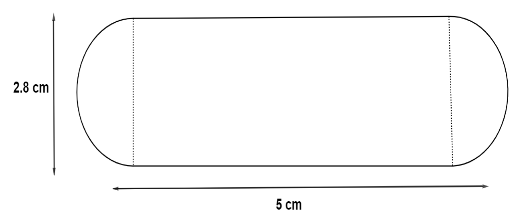
A gulab jamun contains sugar syrup up to about \[30\% \] of its volume. Find approximately how much syrup should be found in \[45\] gulab jamuns, each shaped like a cylinder with two hemispherical ends with a length of \[5\] cm and diameter of \[2.8\] cm as shown in the below figure.

Answer 1

Hint:The given problem is based on the topic surfaces and volumes. From the question and the given figure we can say that a gulab jamun is formed by the combination of a cylinder and hemispheres at both the ends. To find the volume of gulab jamun formed by combining cylinder and hemisphere, find the volume of cylinder and hemisphere separately then add it together. To find the total quantity of sugar syrup in \[45\] gulab jamuns, multiply it with the volume gulab jamun and the sugar syrup in a gulab jamun.

Formulas used:
Volume of the cylinder \[ = \pi {r^2}h\].
Volume of the hemisphere \[ = \dfrac{2}{3}\pi {r^3}\].

Complete step by step answer:
In this problem, we are given that,
Length of the cylinder and hemisphere, \[l = 5\] cm.
Diameter of the cylinder and hemisphere, \[d = 2.8\] cm.
We know that diameter, \[d = 2r\]. Thus the radius, \[r = \dfrac{d}{2}\].
\[r = \dfrac{{2.8}}{2} = 1.4\]
Thus the radius of the cylinder and hemisphere, \[r = 1.4\] cm.
We know the formula that, volume of cylinder \[ = \pi {r^2}h\].
For finding volume we need to find height (\[h\]).
We have one formula, length of the cylinder, \[l = h + 2r\].
\[5 = h + 2(1.4)\]
Thus, \[h = 5 - 2.8 = 2.2\].
The height of the cylinder, \[h = 2.2\] cm.
The volume of cylinder \[ = \pi {r^2}h\]

By substituting values,
\[\text{volume of cylinder} = \pi {(1.4)^2}(2.2)\]
Value of \[\pi \] is \[\dfrac{{22}}{7} = 3.14\]. Let's take \[\pi = \dfrac{{22}}{7}\], which will be easy for further calculation and \[{(1.4)^2} = 1.4 \times 1.4 = 1.96\].
\[\dfrac{{22}}{7} \times 1.96 \times 2.2\]
By doing the calculation we will get \[ 13.552\].
Volume of the cylinder is \[13.552\,cm^3\].
Volume of the hemisphere \[ = \dfrac{2}{3}\pi {r^3}\].
Substituting values,
\[\text{Volume of the hemisphere}= \dfrac{2}{3} \times \pi \times {(1.4)^3}\]
Value of \[\pi = \dfrac{{22}}{7}\] and \[{(1.4)^3} = 1.4 \times 1.4 \times 1.4 = 2.744\]
\[\text{Volume of the hemisphere} = \dfrac{2}{3} \times \dfrac{{22}}{7} \times 2.744\]
\[\Rightarrow \text{Volume of the hemisphere} = \dfrac{{120.736}}{{21}}\]

By dividing we will get, \[ = 5.7493333\], the numbers after decimal are recurring so rounding we will get.Therefore, Volume of the hemisphere is \[5.75\,cm^3 \].
As per the diagram our gulab jamun has two hemispheres, then the volume of two hemispheres \[ = 2 \times 5.75 = 11.5\,cm^3 \].
And now the volume of gulab jamun \[ = \] volume of cylinder \[ + \] volume of hemispheres.
\[\text{volume of gulab jamun}= 13.552 + 11.5\]
\[\therefore \text{volume of gulab jamun} = 25.052\]
Volume of one gulab jamun is \[25.052\,cm^3\].
Sugar syrup in one gulab jamun \[ = 30\% = \dfrac{{30}}{{100}} = 0.3\]
Sugar syrup in \[45\] gulab jamuns \[ = 45 \times 0.3 \times 25.052\]\[ = 338.202\]
Hence the quantity of sugar syrup contained in \[45\] gulab jamuns is \[228.202\,{cm^3}\].

Note: If an object is formed by the combination of two or shapes then its surfaces and volumes can be found by calculating the surface and volume of each shape separately and adding those results together we will get the surfaces and volumes of that particular object.