Question

A gets as many marks less than B as B gets less than C. If the total marks of A, B and C is 270 and C got 90 marks more than A, then find the marks secured by them individually.
[a] 30,60,180
[b] 45,90,135
[c] 40,80,150
[d] 35,70,165

Answer 1

Hint: Assume that the marks of A be x and the marks of B be y. Let the marks of C be x+90. From the statement of the question form two linear equations in two variables x and y. Solve for x and y using the substitution method or the elimination method or using the graphical method and hence find the marks of A, B and C.

Complete step-by-step solution -

Let the marks secured by A be x and the marks secured by B be y. Since C secures 90 marks more than A marks secured by C = x+90.
Since A gets as many marks less than B as B gets less than C, we have
y-x = x+90-y
Adding y on both sides, we get
2y-x = x+90
Adding x on both sides, we get
2y = 2x+90
Dividing by 2 on both sides, we get
y = x+45 (i)
Also, the total marks secured by all of them are 270. Hence we have
x+y+x+90 = 270
2x+y+90 = 270
Subtracting 90 from both sides, we get
2x+y = 180 (ii).
Substituting the value of y from equation (i), we get
2x+(x+45) = 180
i.e. 3x+45 =180
Dividing both sides by 3, we get
x+ 15 = 60
Subtracting 15 from both sides, we get
x = 45
Substituting the value of x in equation (i), we get
y =45+45 = 90
Hence the marks secured by C are 45+90 = 135
Hence the marks secured by A are 45, the marks secured by B are 90 and the marks secured by C are 135.
Hence option [b] is correct.

Note: Plotting equation (i) and (ii) on a graph paper:
The graph is shown below

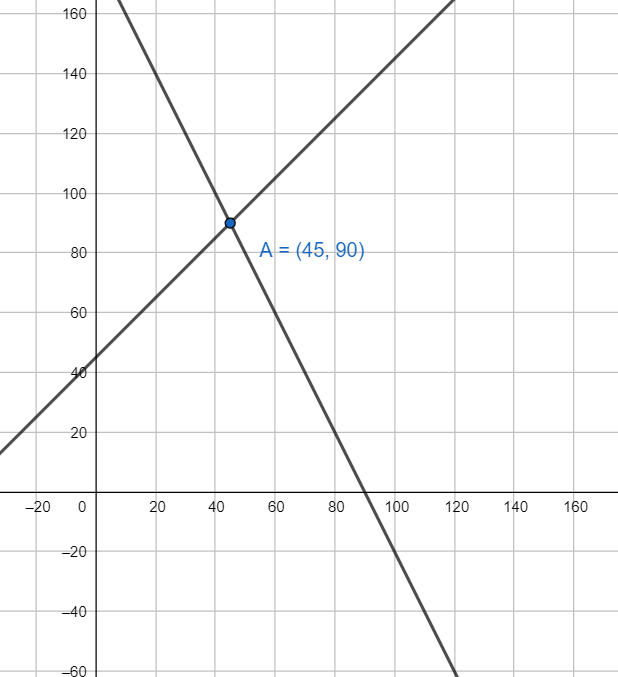
As is evident from the graph that the lines intersect at (45,90)
Hence x = 45 and y = 90, which is the same as obtained above.