Question

A geostationary satellite is orbiting around the earth at a height of 30,000 km in a circular orbit. The radius of the earth is taken as 6000 km. The geostationary satellite comes back to its position after one revolution in exactly 24 hours. Let the acceleration due to gravity (g) be 10m/s2 and the mass of the satellite be 1000 kg; calculate the work done in 12 hours when moving under gravitational force?
(A) \[3.6\pi \times \mathop {10}\nolimits^{14} \] J
(B) \[2\pi \times 7.2\pi \times \mathop {10}\nolimits^{14} \] J
(C) \[1.8\pi \times \mathop {10}\nolimits^{14} \] J
(D) 0J

Answer 1

Hint: This problem can be solved by the concept of gravitational potential energy. As we know the gravitational potential energy of a body at a point in a gravitational field of another body is defined as the amount of work done in bringing the given body from infinity to that point.

Complete step by step answer:
Step 1:

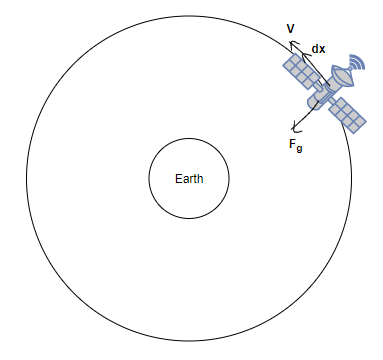
The gravitational force of attraction on the body at the point A will be equal to \[\mathop F\nolimits_g \]. Where \[\mathop F\nolimits_g \] can be defined as-
\[\mathop F\nolimits_g = \dfrac{{GMm}}{{\mathop x\nolimits^2 }}\] (1)
Where \[G = \]Universal Gravitational constant, \[M = \]Mass of earth, \[m = \]Mass of geostationary satellite, and \[x = \]distance between the earth and the satellite
Step 2:
We know that the work done by the satellite in 12 hours moving under the gravitational force can be defined as the integration over initial to final limits of the quantity given by the dot product of gravitational force and displacement of the satellite at that instant.
\[\int_i^f W = \int_i^f {\mathop F\nolimits_g \cdot dx} \]
\[\int_i^f W = \int_i^f {\mathop F\nolimits_g dx} \cos \theta \]
\[\theta = 90^\circ \] because the gravitational force is perpendicular to the displacement of the satellite at each and every point due to circular motion of the satellite and it can be seen from the above figure.
And we know that \[\cos 90^\circ = 0\]
\[\mathop W\nolimits_t = 0\] J

$\therefore $ The total work done by the satellite in 12 hours is \[0\]J. The correct option is (D).

Note:
(i) The direction of displacement at any instant in a circular motion is given by the tangent at that point.
(ii) While calculating the work done one should have to keep the point in mind that work done is a scalar quantity but it is the dot product of two vector quantities. So scalar products should be taken instead of multiplication.