Question

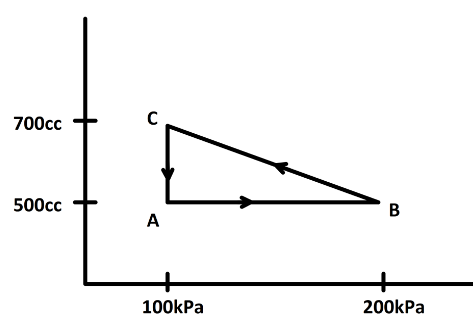
A gas is taken through a cyclic process ABCA as shown in figure. If \[2.4\,cal\] of heat is given in the process. Then, what is the value of \[J\]?

Answer 1

Hint: From the second law of thermodynamics, we know that the energy given to a system is used in two ways. One is used to increase the internal energy of the system and the other part is used to do some work done by the system.

Formula used: The second law of thermodynamics is given by,
\[dQ = dU + dW\]
where \[dQ\] is the energy given to the system \[dU\] is the change in internal energy of the system and \[dW\] is the work done by the system.
Area of a right angle triangle is, \[A = \dfrac{1}{2} \times Base \times Height\]

Complete step by step answer:
We know from the second law of thermodynamics that the work done by a system is the difference between the energy given to the system and the change in internal energy of the system. \[dQ = dU + dW\] where \[dQ\]is the energy given to the system \[dU\] is the change in internal energy of the system and \[dW\] is the work done by the system.

Now, from the $P-V$ curve we can find the work done by calculating the area under the curve. here we have a cyclic process $ABCA$. Now, in a cyclic process we know the state of the system does not change. So, change in internal energy is zero. Now, the area under the curve is the difference between the area $DBCE$ and the area $DACE$ or the area of the triangle $ABC$

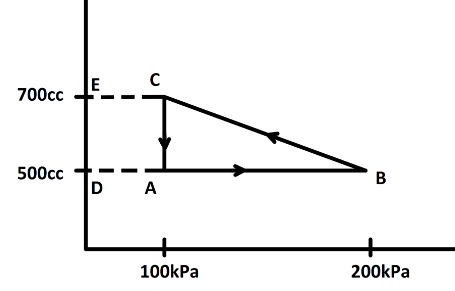
So, the area of triangle ABC will be,
\[\dfrac{1}{2} \times (200 - 100) \times {10^3} \times (700 - 500) \times {10^{ - 6}}J\] [Since, \[1cc = {10^{ - 6}}{m^3}\] and \[1kPa = {10^3}Pa\]]
Upon simplifying we have,
\[ \text{area of triangle ABC}= \dfrac{1}{2} \times 100 \times {10^3} \times 200 \times {10^{ - 6}}J\]
\[ \Rightarrow \text{area of triangle ABC}= 100 \times 100 \times {10^{ - 3}}J\]
\[ \Rightarrow \text{area of triangle ABC}= 10\,J\]
Now, we have given that \[2.4cal\]heat is given to the system so, we can write,
\[2.4J = 10\] [Since, \[dU = 0\]]
\[\therefore J = \dfrac{{10}}{{2.4}} = 4.166\]

Hence, the value of \[J\] is \[4.17J \cdot ca{l^{ - 1}}\].

Note: The work done by the system is the area under the P-V curve .Here we have given V-P curve. Also, to find the area under a P-V curve we just integrate as, \[W = \int {PdV} \]Where, \[P\] is a function of \[V\]and \[T\], and \[dV\]is the change in volume for a work done \[dW\].