Question

A garden measuring \[12m\] by \[16m\] is to have a pedestrian pathway that is \[w\] meters wide installed all the way around so that it increases the total area to \[285{m^2}\]. What is the width of the pathway?

Answer 1

Hint: In the given question, we have been given that there is a garden of some given measurement. There is a figure constructed around the rectangular garden of some given width. The figure adds some area and makes the total area equal to the given quantity. We have to find the width. This can be easily calculated by first drawing the figure, marking the measurements, and applying the formula. Then just simplification is needed, and we will get the answer.
Formula used:
We are going to use the formula of area of rectangle,
\[A = length \times breadth\]

Complete step by step solution:

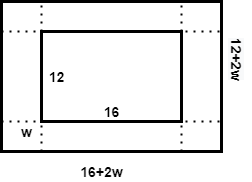
According to the given question,
\[\left( {12 + 2w} \right)\left( {16 + 2w} \right) = 285\]
Simplifying,
\[192 + 56w + 4{w^2} = 285\]
or \[4{w^2} + 56w - 93 = 0\]
Solving the equation by using the quadratic formula,
\[w = \dfrac{{ - 56 \pm \sqrt {{{\left( {56} \right)}^2} - 4 \times \left( { - 93} \right) \times 4} }}{8} = \dfrac{{ - 56 \pm \sqrt {4624} }}{8} = \dfrac{{ - 56 \pm 68}}{8}\]
But width cannot be negative, so
\[w = \dfrac{{ - 56 + 68}}{8} = \dfrac{{12}}{8} = 1.5m\]

Note: In the given question, we had been given a garden of some given measurements. We had to calculate the width of the figure constructed around it. To do that, we first drew the figure. Then we marked the measurements, applied the formula and calculated the answer.