Question

A galvanometer has a current sensitivity of 1mA per division. A variable shunt is connected across the galvanometer and the combination is put in series with a resistance of $500\Omega $ and a cell of internal resistance $1\Omega $. It gives deflection of 5 divisions for shunt of 5 ohms and 20 divisions for shunt of 25 ohm. The emf of cell is
A. 47.1V
B. 57.1V
C. 67.1V
D. 77.1V

Answer 1

Hint: Find the current flowing through the circuit for the two conditions given in the question. Obtain the emf equation for the given circuit and then values of the current flow for the two conditions to get two equations. Solve these two equations to find the emf of the cell.

Complete answer:
Draw the circuit diagram according to the given condition.

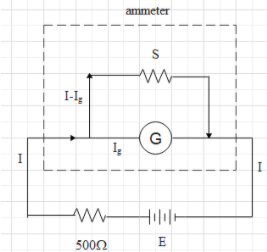
Let the current through the resistance is I and the current through the galvanometer is ${{I}_{g}}$. Then the current passing through the shunt will be $I-{{I}_{g}}$.
Now, we can write that,
\[\begin{align}
  & {{R}_{g}}{{I}_{g}}=S\left( I-{{I}_{g}} \right) \\
 & I=\dfrac{{{I}_{g}}\left( {{R}_{g}}+S \right)}{S} \\
\end{align}\]
Where, ${{R}_{g}}$ is the resistance of the galvanometer and S is the resistance of the shunt.
Now, when the shunt is 5 ohms, deflection in the galvanometer is 5.
So, $S=5\Omega $s and ${{I}_{g}}=5mA$
We can write,
$\begin{align}
  & {{I}_{1}}=\dfrac{5\left( {{R}_{g}}+5 \right)}{5} \\
 & {{I}_{1}}={{R}_{g}}+5 \\
\end{align}$
Again, when the shunt is 25 ohms, deflection in the galvanometer is 20.
So, $S=25\Omega $s and ${{I}_{g}}=20mA$
We can write,
\[\begin{align}
  & {{I}_{2}}=\dfrac{20\left( {{R}_{g}}+25 \right)}{25} \\
 & {{I}_{2}}=0.8\left( {{R}_{g}}+25 \right) \\
 & {{I}_{2}}=0.8{{R}_{g}}+20 \\
\end{align}\]
Now, the combination is connected in series with a resistance of 500 ohms and a cell of internal resistance 1 ohm.
So, $R=500\Omega $ and $r=1\Omega $
So, the emf of the cell can be expressed as,
$\begin{align}
  & E=\left( R+r \right)I+{{I}_{g}}{{R}_{g}} \\
 & E=501I+{{I}_{g}}{{R}_{g}} \\
\end{align}$
Now, substituting ${{I}_{1}}$ in the emf equation, we get that,
$\begin{align}
  & E=501\left( {{R}_{g}}+5 \right)+5{{R}_{g}} \\
 & E=2505+506{{R}_{g}} \\
\end{align}$
Again, substituting ${{I}_{2}}$ in the emf equation, we get that,
$\begin{align}
  & E=501\left( 0.8{{R}_{g}}+20 \right)+5{{R}_{g}} \\
 & E=10020+420.8{{R}_{g}} \\
\end{align}$
Solving the above two equation, we get that,
$\begin{align}
  & E=47136mV \\
 & E\sim 47.1V \\
\end{align}$
The emf of the cell is 47.1 V.

The correct option is (A).

Note:
When the current through a circuit divides at a point in a circuit and then adds up at another point, the potential difference between these two points across the two different paths will be the same. Using this concept, we have put the equations in the above question.