Question

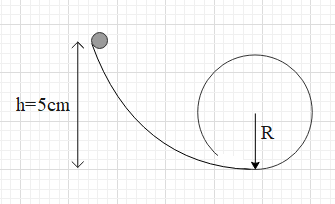
A frictionless track ABCDE ends in a circular loop of radius R. A body slides down the track from point A which is at height h=5cm. Maximum value of R for the body to successfully complete the loop is :

 $\text{A}\text{. }5cm$
$\text{B}\text{. 2}cm$
$\text{C}\text{. }\dfrac{10}{3}cm$
$\text{D}\text{. }\dfrac{15}{4}cm$

Answer 1

Hint: For the body to successfully complete the circular loop, its minimum speed at the bottom of the loop, when it enters the loop must be equal to $\sqrt{5gR}$. Use the work energy theorem, calculate the speed of the body when it comes down from a height of 5cm. This speed must be greater than $\sqrt{5gR}$. Solving the inequality, you will get the maximum value of R.

Formula used:
W=mgh
$K=\dfrac{1}{2}m{{v}^{2}}$

Complete answer:
In the given figure, the body is initially at a height of h = 5cm, at the top of the track. Since there is no friction, the body will slide down the track under the influence of the gravitational force only.
Due to the gravitational force the body will accelerate as it comes down. Hence, it will have some velocity when it reaches the bottom of track. Let that velocity be v.
Now the condition is that the body must successfully complete the circular loop of radius R. If the body has to successfully complete the loop then the minimum required speed when it enters the circular loop is $\sqrt{5gR}$, where g is acceleration due to gravity.
This means that the minimum of $v=\sqrt{5gR}$.
$\Rightarrow v$ > $\sqrt{5gR}$.
Let us calculate the value of v.
Since the body comes down under the gravitational force, the gravitational force will do a positive work on the body, which will be equal to W=mgh.
Here, m is the mass of the body.
From the work-energy theorem, the work done is equal to the change in kinetic energy of a body.
i.e. $W=\Delta K$.
In this case, $\Delta K=\dfrac{1}{2}m{{v}^{2}}$.
Therefore,
$mgh=\dfrac{1}{2}m{{v}^{2}}$
$\Rightarrow v=\sqrt{2gh}$.
Here, h=5cm.
$\Rightarrow v=\sqrt{2gh}=\sqrt{2g(5)}=\sqrt{10g}$.
But we know that v > $\sqrt{5gR}$.
This means that
$\sqrt{10g}$ > $\sqrt{5gR}$.
$\Rightarrow 10g$ > $5gR$
$\Rightarrow R$ < 2cm.
This means that for the body to successfully complete the loop, the radius of the loop must be less than 2cm.
Therefore, the maximum value of R is 2cm.

Hence, the correct option is B.

Note:
Other than the work-energy theorem, we can also apply the law of conservation of mechanical energy.
Since gravity is conservative force, the mechanical energy of the system will be conserved.
In the words, the negative change in potential of the body is equal to the change in its kinetic energy.
i.e. $\Delta K=-\Delta U$.
Since the body comes down by an height h, the change in potential energy of the body is $\Delta U=-mgh$
$\Rightarrow \dfrac{1}{2}m{{v}^{2}}=-(-mgh)$
$\Rightarrow {{v}^{2}}=2gh$
$\Rightarrow v=\sqrt{2gh}$.