Question

A freely moving piston divides a vertical cylinder closed at both ends, into two parts each containing $1$ mole of air. In equilibrium, at $$T=300K$$, volume of the upper part is $4$ times greater than the lower part. At what temperature will the ratio of these volumes be equal to $2$?

Answer 1

Hint: Since the problem involves gases in a closed cylinder there is a pressure and a corresponding force associated with it. The equation based on the concept of equilibrium is applied in order to determine the forces exerted by the gases on the piston considering the mass of the piston as well which will give the equations relating the pressures at the two conditions of temperatures. The ideal gas equation is then applied in order to determine the required temperature.

Formula used:
The ideal gas equation is given by:
$PV=nRT$
Where, $P$ is the pressure of the gas, $V$ is the volume of the gas, $n$ is the number of moles, $R$ is the gas constant and $T$ is the temperature.

Complete step by step answer:
 When a piston is placed inside a cylinder which is closed at both ends then the piston divides the air or the gas inside the cylinder so that there is some amount of gas present above the piston and the remaining amount of gas present below the piston. Hence, the concept of pressure comes into picture because the molecules of the gas particles present above and below the piston are bound to exert a force on the piston because pressure is said to be the force exerted by a gas per unit area

The diagram below illustrates how the piston has divided the cylinder into two portions:

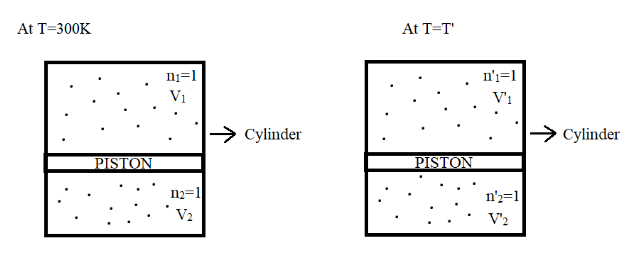
The problem takes two temperature conditions into consideration, that is, one at $T=300K$ and another condition whose temperature we need to find. Let us now take the case for the temperature condition $T=300K$.

There will be a certain amount of force that will be exerted on the piston by the air molecules present in the upper part of the cylinder. Similarly there will be a force that is exerted by the piston on the lower portion of the gas molecules as well. Hence, to balance out these forces an upward force will be exerted by the gas molecules present in the lower portion of the cylinder. This is where the concept of equilibrium comes into picture.

Therefore, by the concept of equilibrium the force exerted by the upper portion and the force applied by the piston will be equivalent to the force exerted by the lower portion of the cylinder.From the above discussed concept we can construct an equation:
$F_{upper}+F_{piston}=F_{lower}$
Where, $F_{upper}$ is the force exerted by the gas molecules present above the piston, $F_{lower}$ is the force exerted by the gas molecules present below the piston and $F_{piston}$ is the force exerted by the piston.
Hence by writing the above equation in terms of pressure and area we get:
$P_1{A}_1+mg=P_2{A}_2$ [Since, we know that $F=P\times A$ and also $F=mg$]
$\Rightarrow mg=P_2{A}_2-P_1{A}_1$ -------($1$)
Where, $P_1$ is the pressure of the gas molecules present above the piston, $A_1$ is the area of upper portion of piston, $P_2$ is the pressure of the gas molecules present below the piston and $A_2$ is the area of lower portion of piston.

Clearly, the force exerted by the piston is simply the gravitational force. Here, $A_1$ is the area upon which the force $F_{upper}$ is acting while $A_1$ is the area upon which the force $F_{upper}$ is acting. Hence, it can be seen that for an amount of pressure to exist there must be an area on which the force is exerted on.

Similarly let us now take the condition in which the temperature is changed. The equation for the force exerted by the gases at this changed temperature will be different since the gases will have more energy now and hence the pressure of the gases at this condition also changes. The equation becomes:
${P_1}^{\prime }{A}_1+mg={P_2}^{\prime }{A}_2$
$\Rightarrow mg={P_2}^{\prime }{A}_2-{P_1}^{\prime }{A}_1$ -------($2$)
Since the same piston is being used with a variation of only the temperature conditions the area and the force exerted by the piston will remain unchanged.
Since ($1$) and ($2$) are identical we equate them to get:
$\Rightarrow P_2{A}_2-P_1{A}_1={P_2}^{\prime }{A}_2-{P_1}^{\prime }{A}_1$
Since the area of the piston is the same everywhere we get:
$\Rightarrow P_{2}A-P_{1}A={P_2}^{\prime }A-{P_1}^{\prime }A$

The common terms are cancelled out to get:
$\Rightarrow P_2-P_1={P_2}^{\prime }-{P_1}^{\prime }$------($3$)
This is the equation relating the pressures of the gases at the two temperature conditions.
Now, let us come to the volume of these gases at the two temperature conditions. For the temperature condition where $T=300K$, the volume occupied by the gases are given to be related to each other in the question. The volume of the upper part, say $V_2$, is equivalent to four times the volume of the gas at the lower part, say $V_1$.
Hence we get the relation,
$V_2=4V_1$ ------($4$)
When the temperature changes it changes the volume of the gases as well. For the changed temperature condition, the volume of the upper part, say ${V_2}^{\prime }$, is given to be equivalent to two times the volume of the gas at the lower part, say ${V_1}^{\prime }$.
${V_2}^{\prime }=2{V_1}^{\prime }$------($5$)
We now apply the ideal gas equation. The equation is as follows:
$PV=nRT$
By rearranging the terms we get:
$P={\displaystyle \frac{nRT}{V}}$

The above ideal gas equation is now substituted in equation ($3$) and we get:
${\displaystyle \frac{n_{2}R{T}_0}{V_2}}-{\displaystyle \frac{n_{1}R{T}_0}{V_1}}={\displaystyle \frac{{n_2}^{\prime }R{T}^{\prime }}{V_2}}-{\displaystyle \frac{{n_1}^{\prime }R{T}^{\prime }}{{V^{\prime }}_1}}$
Where, $T_0$ is the first temperature condition and $T^{\prime }$ is the second temperature condition which we must find.
Here, the $R$ value is said to be a constant value; the number of moles is said to be $1$ at all conditions. Since $n_1=n_2={n_1}^{\prime }={n_2}^{\prime }=1$ we get the equation as:
${\displaystyle \frac{1\times R{T}_0}{V_2}}-{\displaystyle \frac{1\times R{T}_0}{V_1}}={\displaystyle \frac{1\times R{T}^{\prime }}{{V_2}^{\prime }}}-{\displaystyle \frac{1\times R{T}^{\prime }}{{V^{\prime }}_1}}$
By cancelling out the common terms we and substituting the value of $T_0=300K$ in the above equation we get:
${\displaystyle \frac{300}{V_2}}-{\displaystyle \frac{300}{V_1}}={\displaystyle \frac{T^{\prime }}{{V_2}^{\prime }}}-{\displaystyle \frac{T^{\prime }}{{V^{\prime }}_1}}$
We now substitute the equations ($4$) and ($5$) in the above equation to get:
${\displaystyle \frac{300}{4V_1}}-{\displaystyle \frac{300}{V_1}}={\displaystyle \frac{T^{\prime }}{2{V_1}^{\prime }}}-{\displaystyle \frac{T^{\prime }}{{V^{\prime }}_1}}$ ------($6$)

We now determine an equation relating the volumes of the gases in the second temperature condition with the volumes of the gases at $T=300K$. The volumes of the gases are said to be equal at all times since the same container and piston is used with only a change in temperature. The volume just gets divided by the piston into two portions.
This means that the total volume of the cylinder at $T=300K$ will be equal to the total volume of the cylinder at $T^{\prime }$ temperature. Hence we can say that:
$4V_1+V_1=2V_1^{\prime }+{V_1}^{\prime }$
By solving out the equation we get:
$5V_1=3{V_1}^{\prime }$
$V_1={\displaystyle \frac{3}{5}}{V}_1^{\prime }$ -----($7$)

By substituting equation ($7$) in ($6$) we get:
${\displaystyle \frac{300}{4\times {\displaystyle \frac{3}{5}}{V_1}^{\prime }}}-{\displaystyle \frac{300}{{\displaystyle \frac{3}{5}}{V^{\prime }}_1}}={\displaystyle \frac{T^{\prime }}{2{V_1}^{\prime }}}-{\displaystyle \frac{T^{\prime }}{{V^{\prime }}_1}}$
By taking the common terms out we get:
${\displaystyle \frac{300}{{V_1}^{\prime }}}\left[{\displaystyle \frac{1}{{\displaystyle \frac{12}{5}}}}-{\displaystyle \frac{1}{{\displaystyle \frac{3}{5}}}}\right]={\displaystyle \frac{T^{\prime }}{{V_1}^{\prime }}}\left[{\displaystyle \frac{1}{2}}-1\right]$
The common term ${V_1}^{\prime }$ is then cancelled out:
$\Rightarrow 300\left[{\displaystyle \frac{5}{12}}-{\displaystyle \frac{5}{3}}\right]=T^{\prime }\left[{\displaystyle \frac{1}{2}}-1\right]$
$\Rightarrow -300\times {\displaystyle \frac{15}{12}}=-{\displaystyle \frac{T^{\prime }}{2}}$
The negative signs are cancelled out to get:
$\Rightarrow 300\times {\displaystyle \frac{15}{12}}={\displaystyle \frac{T^{\prime }}{2}}$
We solve out the equation by cross multiplying the terms to get the value of $T^{\prime }$ which is our required temperature:
$\Rightarrow T^{\prime }={\displaystyle \frac{300\times 15\times 2}{12}}$
$\Rightarrow T^{\prime }={\displaystyle \frac{9000}{12}}$
$\therefore T^{\prime }=750K$
This is the second temperature condition which we were required to find.

Note: The volume of the gas is said to be the volume of the container in which it is confined in. The common mistake in this problem is that the force exerted by the two portions of the gas particles are equated and the force of the piston is not considered, which is wrong. The piston also has a mass and hence the gravitational force is exerted on the gas molecules.