Question

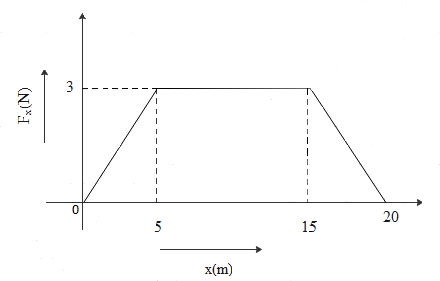
A force \[{{F}_{x}}\] acts on a particle such that its position x changes as shown in figure. The work done by the particle as it moves from \[x=0\text{ to 20}m\] is

\[\begin{align}
  & \text{A}\text{. }37.5J \\
 & \text{B}\text{. }10J \\
 & \text{C}\text{. }15J \\
 & \text{D}\text{. }22.5J \\
 & \text{E}\text{. }45J \\
\end{align}\]

Answer 1

Hint: Here we have given a graph between force and displacement and we have to find the work done. We can find the area of the graph by dividing it into three parts and can find the total work done. To understand properly we can name and points and specify the area or the part of the graph.
Formula used:
\[\begin{align}
  & \text{Work done=Area under the graph }{{F}_{x}}\text{-}x \\
 & \text{Area of triangle=}\dfrac{1}{2}\times \text{base}\times \text{height} \\
 & \text{Area of rectangle =length}\times \text{breadth} \\
\end{align}\]

Complete answer:
Work done is the product of force and displacement, it tells us about the work which is done to change the position of an object. As here, we have given a graph therefore we will just find the area under the graph and it will tell us the amount of work done.
.

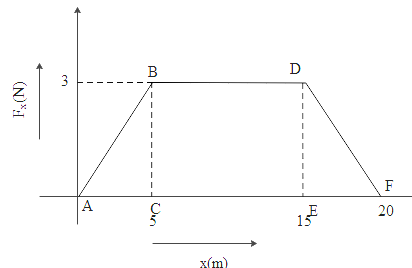
From the graph,
\[\text{Work done=Area of triangle ABC+ Area of rectangle BDEC+ Area of triangle EDF}\]
Here AC is the base of triangle ABC and BC is height of triangle ABC, CE is the length of the rectangle BDEF and DE is the breadth of rectangle BDEF, DE is height of triangle EDF and EF is the base of the triangle EDF. Hence we can write

\[\text{Work done=}\left( \dfrac{1}{2}\times \text{AC}\times \text{BC} \right)\text{+ }\left( \text{CE}\times \text{DE} \right)\text{+}\left( \dfrac{1}{2}\times \text{EF}\times \text{DE} \right)\]
Where, \[\text{AC=EF=}5m\text{, BC=DE=}3m\text{, CE=10}m\]

Substituting the values we get
\[\begin{align}
& \text{Work done=}\left( \dfrac{1}{2}\times 5\times 3 \right)\text{+ }\left( 10\times 3 \right)\text{+}\left( \dfrac{1}{2}\times 5\times 3 \right) \\
 & \text{Work done=}\left( \dfrac{15}{2} \right)\text{+}\left( 30 \right)\text{+}\left( \dfrac{15}{2} \right) \\
 & \text{Work done=45}J \\
\end{align}\]

So, the correct answer is “Option E”.

Note:
From the graph we can also find the work done just to move a particle from zero to five meters or from five to fifteen meters or fifteen to twenty meters. For example, the area of the triangle ABC gives us the amount of work done by a particle to move from zero to five meters. Similarly we can find the work done for any specific area.