Question

A fire in a building B is reported on telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observed that the fire is at an angle of ${60^ \circ }$ to the road and Q observes that it is at an angle of ${45^ \circ }$ to the road. Which station should send its team and how much will this team have to travel.

Answer 1

Hint-Here we will proceed by converting the given conditions into the triangle such that we use trigonometry functions i.e. tan (tangent) where angles will be used as degrees of distance to find the actual distance. Also we must know the common degrees of trigonometric functions as the question states the angle of the buildings i.e. ${60^ \circ },{45^ \circ }$.

Complete Step-by-Step solution:

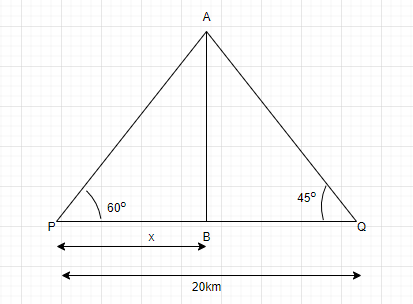
Here we are given that-
AB is the height of Building.
PB is the distance of fire station P from the building.
QB is the distance of fire station Q from the building.
Distance between P and Q is 20 m.
Now, let us assume PB = x
So, QB = 20-x
$ \Rightarrow $ In $\vartriangle APB$,
We will use Tangent function of trigonometry with ${60^ \circ }$.
Formula of tan${60^ \circ }$= $\dfrac{{Perpendicular}}{{Base}}$ = $\sqrt 3 $
$ \Rightarrow $$\sqrt 3 $= $\dfrac{{AB}}{x}$ ………..(1)
$ \Rightarrow $In $\vartriangle ABQ$,
We will use Tangent function of trigonometry with ${45^ \circ }$.
$ \Rightarrow $Formula of tan${45^ \circ }$ = $\dfrac{{Perpendicular}}{{Base}}$= $\dfrac{{AB}}{{BQ}}$
$ \Rightarrow $20 - x = AB ……………… (2)
So comparing 1 and 2,
We get
$ \Rightarrow 20 - x = \sqrt 3 x$x
Or ($20 = \left( {\sqrt 3 + 1} \right)x$
Or $\dfrac{{20}}{{\left( {\sqrt 3 + 1} \right)}} = x$
$ \Rightarrow $x = 7.320
So PB = 7.320 km
Also QB = 20 – 7.320
$ \Rightarrow $QB = 12.68 km
Therefore, fire stations should send a team to Station P since the distance between building and P station i.e. 7.32 km is less than the distance between Q station and building i.e. 12.68 km.
$\therefore $ Team has to travel 7.320 km
Note- In order to solve this question, one can get confused about choosing the right trigonometric function as there are six functions which are sine, cosine, tangent, cosecant, secant and cotangent. Also we must know all the trigonometric ratios which will be used as angles to get the required answer.