Question

A field is 120 m long and 50 m broad. A tank 24m long, 10 m broad and 6 m deep is dug anywhere in the field and the earth taken out of the tank is evenly spread over the remaining part of the field. Find the rise in level (in cm) of the field.

Answer 1

Hint: Let us assume the rise in level of the field be x m. Now, the field is having some height. Get the volume of the field using the formula, \[\text{Volume=Length }\!\!\times\!\!\text{ Width }\!\!\times\!\!\text{ Height}\] . The given tank is also having length, width and height. Now, get the volume of the tank. As much as the volume is removed, the same volume is spread over the field. Therefore, the volume of the tank must be equal to the volume of the field. Now, get the value of x. Using the relation, 100 centi-meter = 1 meter converts the value of x in centi-meter.

Complete step-by-step solution -

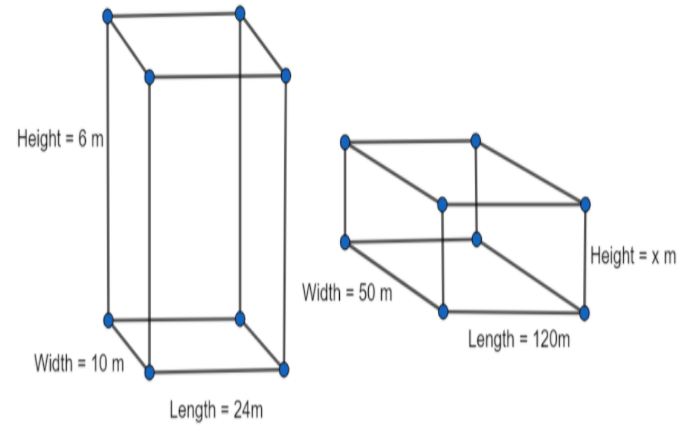
Let the rise in level of the field be x m.
The height of the field = x m.
The length of the field = 120 m.
The width of the field = 50 m.
We know the formula, \[\text{Volume=Length }\!\!\times\!\!\text{ Width }\!\!\times\!\!\text{ Height}\] .
Volume of the tank = \[120\times 50\times x\,{{m}^{3}}\] ……………….(1)
The length of the tank = 24 m.
 The width of the tank = 10 m.
The height of the tank = 6 m.
We know the formula, \[\text{Volume=Length }\!\!\times\!\!\text{ Width }\!\!\times\!\!\text{ Height}\] .
Volume of the tank = \[24\times 6\times 10\,{{m}^{3}}\] ……………….(2)
The tank is dug in the field and the earth taken out of the tank is evenly spread over the remaining part of the field. Initially, the field has only length and width. But after spreading the earth, there is a certain rise in the level of the field. Now, the field has height also. So, as much as the volume is removed, the same volume is spread over the field. Therefore, the volume of the tank must be equal to the volume of the field.
From equation (1) and equation (2), we have the volume of the tank and the volume of the field,
Volume of the tank = Volume of the field
\[\begin{align}
  & 24\times 6\times 10\,{{m}^{3}}=120\times 50\times x\,{{m}^{3}} \\
 & \Rightarrow \dfrac{24\times 6\times 10}{120\times 50}=x \\
 & \Rightarrow \dfrac{6}{5\times 5}=x \\
 & \Rightarrow \dfrac{6}{25}=x \\
\end{align}\]
The value of rise in level of the field is \[\dfrac{6}{25}\,m\] …………..(3)
We have to find the rise in level in “cm”.
We know the relation between “m” and “cm”.
100 cm = 1 m ………………….(4)
From equation (3) and (4), we have
\[\dfrac{6}{25}\,m=\dfrac{6}{25}\times 100\,cm=6\times 4\,cm=24\,cm\] .
Hence, the value of rise in level of the field is \[24\,cm\] .

Note: We can also solve this question, by direct formula, The rise in the level of the field = \[\dfrac{\text{Volume}\,\text{of the tank}}{\text{Area of the field}}\]=\[\dfrac{24\times 6\times 10}{120\times 50}=\dfrac{6}{5\times 5}=\dfrac{6}{25}\]m.
In this question, one might conclude \[\dfrac{6}{25}\,m\] as an answer which is wrong. In the question, the value of rise in level of the field is asked in centi-meters. So, using the relation, 100 cm = 1 m , convert the unit of meter into centi-meters and then conclude the answer.