Question

A field in the form of a quadrilateral ABCD whose sides taken in order are respectively equal to 192dm,576dm,288dm and 480dm has the diagonal equal to 672dm. Its area to the nearest square metre is 1011.

Answer 1

Hint:The given quadrilateral is not in any shape of rectangle or square. So, draw diagonal to get two triangles. Using Heron’s formula, find the area of both triangles. Add both areas to get the total area of ABCD.

Complete step-by-step answer:
First we draw the diagram for ABCD quadrilateral. Its diagonal is AC.

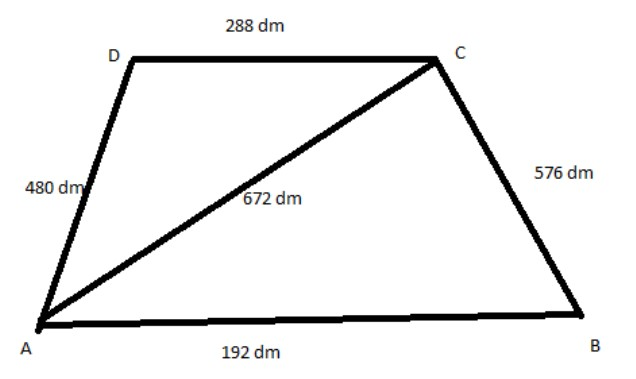
The data given in the problem is as:
Side AB = 192 dm
Side AD = 480 dm
Side DC = 288 dm
Side BC = 576 dm
And Diagonal AC = 672 dm.
We consider two triangles ADC and ACB one by one , to compute their areas.
In $\vartriangle ADC$,
Semi perimeter = $\dfrac{{side1 + side2 + side3}}{2}$
s = $\dfrac{{AD + DC + AC}}{2}$
s= $\dfrac{{480 + 288 + 672}}{2}$
So, s = 720 dm
So, area of $\vartriangle ADC$ by Heron’s formula ,
${A_1} = \sqrt {s(s - a)(s - b)(s - c)} $
Here three sides are 480, 288 and 672 and the semi perimeter is 720. So, we have
$
  {A_1} = \sqrt {720 \times (720 - 480) \times (720 - 288) \times (720 - 672)} \\
  {A_1} = \sqrt {720 \times 240 \times 432 \times 48} \\
  {A_1} = 59859.67\;d{m^2} \\
 $
Thus the area of $\vartriangle ADC$ is 59859.67 $d{m^2}$ .
Similarly for the $\vartriangle ACB$ ,
Semi perimeter = $\dfrac{{side1 + side2 + side3}}{2}$
s = $\dfrac{{AC + CB + BA}}{2}$
s= $\dfrac{{672 + 576 + 192}}{2}$
So, s = 720 m
So, area of $\vartriangle ACB$ by Heron’s formula ,
${A_2} = \sqrt {s(s - a)(s - b)(s - c)} $
Here three sides are 192, 576 and 672 and the semi perimeter is 720. So, we have
$
  {A_2} = \sqrt {720 \times (720 - 192) \times (720 - 576) \times (720 - 672)} \\
  {A_2} = \sqrt {720 \times 528 \times 144 \times 48} \\
  {A_2} = 51260.76\;d{m^2} \\
 $
Thus area of $\vartriangle ACB$ is 51260.76 $d{m^2}$ .
Now, we compute the area of ABCD by adding both triangles’ areas, as
Total area = ${A_1} + {A_2}$ = 59859.67 $d{m^2}$ + 51260.76 $d{m^2}$
Total area = 111120.43 $d{m^2}$
Since 1 ${m^2} = 100d{m^2}$
So, total area will be 1111.20 ${m^2}$
$\therefore $ Area of quadrilateral to the nearest square meter will be 1111.

Note:Above geometrical problem is straightforward application of Heron’s formula for computing the triangle area of any shape. Also, some algebraic calculations and square root computations are used here. Remember the units given here for the measurement. So, suitable conversions are important.