Question

A field 360m long and 120m wide has two cross roads in the centre. Each road is 3m wide. Find the area of cross roads.

Answer 1

Hint: To solve this question first we will make the diagram according to the information provided in the question. After that we will find dimensions of both cross roads by observing from figure. After that, we will evaluate the area of both cross roads by adding the area of both cross roads and subtracting the cross section area of $3m\times 3m$.

Complete step by step answer:

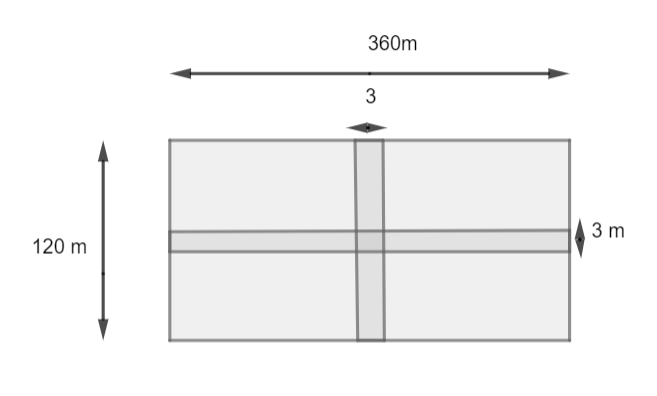
Now, from the figure we can see that there is a rectangular field which has a length of 360m and width of 120m.
Also, we know that the area of the rectangle is equal to $l\times b$ , where l is the length of the rectangle and b is breadth of rectangle.
So, the area of the larger field will be $360m\times 120m$ which is equal to $43,200{{m}^{2}}$.
Now, it is given that there are cross roads at the centre of the field whose width is 3m. It is obvious that the vertical cross road will not exceed the length of the rectangular field and the horizontal cross road will not exceed the measure of width of the rectangular field.
So, from figure we can say that length of vertical ( standing ) road will be 120 m and length of horizontal ( sleeping ) road will be 360 m and width of both roads are same, that is 3 m.
Now, from the figure we can see that in the middle of the field, two cross sections of dimensions $3m\times 3m$ are overlapping each other, where each cross section is of both cross roads. So, we will consider only one cross section.
Hence, we can say that Area of cross roads = Area of vertical cross road + Area of Horizontal Cross road – area of one cross section of dimension $3\times 3$.
So, Area of cross roads \[=~360m\times 3m+120m\times 3m-3m\times 3m\]
On solving, we get
\[=~1080{{m}^{2}}+360{{m}^{2}}-9{{m}^{2}}\]
On simplifying, we get
So, the area of cross roads is $1431{{m}^{2}}$ .

Note: Always draw a figure in these types of question before solving the question as this helps you in visualizing the question perfectly. Do not forget to subtract the area of one cross section from while calculating the area of cross roads as it will change the answer. Do not forget to put units of area and length after numerical values. Try not to make any calculation mistakes.