Question

A farmer connects a pipe of internal diameter 20cm from a canal into a cylindrical tank in his field, which is 10m in diameter and 2m deep. If water flows through the pie at the rate of $3km{{h}^{-1}}$ , in how much time will the tank be filled?

Answer 1

Hint: Volume of a cylinder is $\pi {{R}^{2}}H$ where $\pi $is $\dfrac{22}{7}$ , R is the radius and H is the height of the cylinder. Pipe and tank both are of cylindrical shape. Capacity of any solid represents the volume of it. Suppose the time taken to fill the tank by pipe is a variable. Now, calculate the volume flow through the pipe in this variable time and equate it to the volume of the tank.

Complete step-by-step answer:

Here, it is given that the farmer connects the pipe to the cylindrical tank and hence water will flow through the pipe to fill the tank. We know that the capacity of any solid is known as the volume of that solid. So, we can observe that the volume of the tank will be equal to the volume of water flowing through the pipe at the time when the tank will be filled.
So, let us first calculate the volume of the tank. We have a cylindrical tank with diameter 10m and depth 2m. We know the volume of a tank can be given using the formula.
Volume of cylinder $=\pi {{r}^{2}}h$
Where $\pi =\dfrac{22}{7}$
r = radius and h = height or depth
Hence, volume of the tank can be given as
Volume of tank $=\pi {{r}^{2}}h$
We know $\text{radius}=\dfrac{\text{diameter}}{2}$
So, $r=\dfrac{10}{2}=5m$
h = 2m
So, we get
Volume of the given tank
$\begin{align}
  & =\dfrac{22}{7}\times {{5}^{2}}\times 2 \\
 & =\dfrac{22}{7}\times 25\times 2 \\
\end{align}$
Volume of the tank $=\dfrac{1100}{7}{{m}^{3}}.............\left( i \right)$
Now, we know that pipe used to fill the tank will have cylindrical shape also

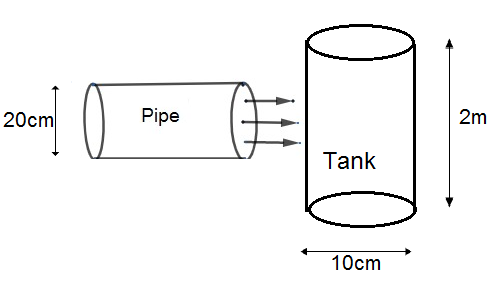
Now, it is given that the rate of flow of water is 3km per hour means water travels 3km in 1 hour.
So, the volume of water in 1 hour inside the pipe can be given by the volume of the cylinder with length 3km and diameter 20cm.
So, let's suppose the pipe is filled in ‘t’ hour. It means water will travel 3km in ‘t’ hour as quantity of water in an hour will flow to 3km. Hence, the volume of the pipe of length ‘3t’ km and diameter 20cm will fill the tank in ‘t’ hour. It means volume in 3t km of the pipe should be equal to the volume of the cylindrical tank.
So, volume of the pipe can be given as
Volume of the pipe $=\pi {{R}^{2}}H$
Where R = radius of the pipe
$\dfrac{20}{2}=10cm$
We know 1m = 100 cm or
$1cm=\dfrac{1}{100}m$
Hence,
$10cm=\dfrac{10}{100}=0.1m$
And length of the pipe taken = 3t km
We know 1km = 1000 m
So,
$\begin{align}
  & 3tkm=3t\times 1000 \\
 & =3000tm \\
\end{align}$
Hence, volume of the pipe,
$\begin{align}
  & \dfrac{22}{7}\times 0.1\times 0.1\times 3000t \\
 & =\dfrac{22}{7}\times 30t..................\left( ii \right) \\
\end{align}$
Now, we can equate the volume of the pipe and tank from the equation (i) and (ii) because of the reason explained above.
So, we get
$\begin{align}
  & \dfrac{1100}{7}=\dfrac{22}{7}\times 30t \\
 & 110=22\times 3t \\
\end{align}$
So, we get
$t=\dfrac{110}{22\times 3}=\dfrac{10}{6}=\dfrac{5}{3}$hour.
Hence, we get time to fill the tank for $\dfrac{5}{3}$ hour.
We know that there are 60 minutes in one hour. So, we can convert ‘t’ in an hour to minutes. So, we get
1 hour = 60 minutes
$\dfrac{5}{3}=\dfrac{5}{3}\times 60=100$
Hence, we get t = 100 minutes or t = 1 hour 40 minutes
So, the answer is 1 hour 40 minutes.

Note: Another approach for solving this question would be that we can equate quantity of water in 1 hour in pipe and cylindrical tank as well. So, here we need to divide the volume of the tank by ‘x’ time to get the volume of water in 1 hour and equate it to the volume of water of pipe in 1 hour. Results will be the same for this approach as well.
Don’t confuse it with the formula of the volume of the cylinder. Be clear with the formula of volumes and surface areas for these kinds of questions. Wrong formulas will give you wrong results.
Use the same units while equating the volumes, only in single units. Either cm or m or km whatever you like but follow only one unit for each quantity. One should be clear with the conversion of the units as well to get the correct answer.