Question

A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftsmen time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftsmen time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmen time.
What number of rackets and bats must be made if the factory is to work at full capacity?
If the profit on a racket and a bat is Rs.20 and Rs.10 respectively, find the maximum profit of the factory when it works at full capacity.

Answer 1

Hint: This is a constraint-based problem, in which one has to make some equations by following the conditions which are given in the question. Finally, we have to solve those equations graphically to find the answers to the questions asked above.

Complete step by step answer:
In the question, it is given that a tennis racket takes 1.5 hours of machine time and 3 hours of craftsman’s time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftsmen time.
Also, in a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmen time.
As the number of tennis rackets and cricket bats is not given in the question, let us assume them.
Let the number of Tennis Rackets be x.
Let the number of Cricket Bats be y.
So, according to the above conditions, let us study the table given below:

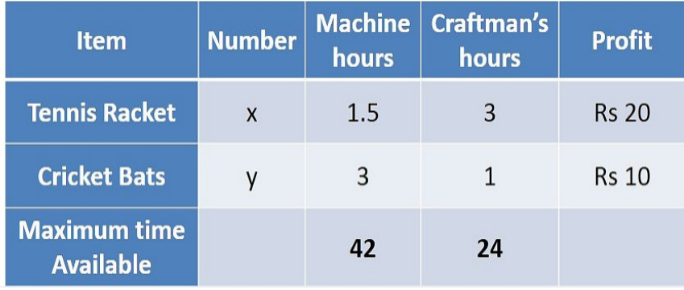
After observing the above table, the conclusion derived can be seen below:
For Machine Hours: Tennis Racket requires- 1.5 hours and Cricket Bat requires- 3 hours
The maximum time available is 42 hours.
$\begin{align}
  & \therefore 1.5x+3y\le 42 \\
 & 3x+6y\le 84 \\
 & \Rightarrow x+y\le 28 \\
\end{align}$
For Craftsman’s Hours: Tennis Racket requires- 3 hours and Cricket Bat requires- 1 hour
The maximum time available is 24 hours.
$\begin{align}
  & \therefore 3x+y\le 24 \\
 & Also,x\ge 0\And y\ge 0 \\
\end{align}$
As we want to maximize the profit, hence the function used here will be to maximize Z.
Profit on each tennis racket is Rs.20 and on each Cricket Bat its Rs.10.
$\therefore MaxZ=20x+10y$
Combining all the constraints:
Maximum Z = 20x + 10y
Subject to constraints:
$\begin{align}
  & x+2y\le 28 \\
 & 3x+y\le 24 \\
 & x\ge 0,y\ge 0 \\
\end{align}$
Hence, based on the above constraints and conditions, we can draw the graph below:

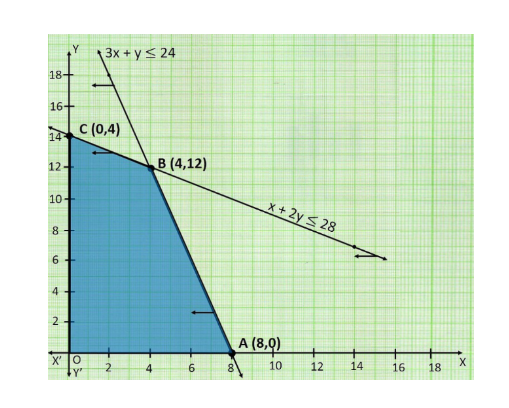
Here, point B i.e. (4, 12) will give the maximum value of Z i.e. 16.
Hence, (i) 4 Tennis rackets and 12 cricket bats must be made so that the factory runs at full capacity.
Hence, (ii) Maximum profit is Rs.200 when 4 tennis rackets and 2 cricket bats are produced.
Note: In these types of questions involving different conditions and constraints, one should always assume some variable to make a graph which will help to solve the question.