Question

a) Draw a graph between spring force \[{F_s}\] and displacement x and
b) Also find an expression for the P.E of an elastic stretched spring.

Answer 1

Hint: To draw the graph between spring force and displacement of the spring, recall Hooke’s law. According to Hooke’s law the spring force is proportional to the displacement of the spring. The area under the curve in the spring force and displacement graph is the potential energy stored in the spring.

Formula used:
Hooke’s law,
\[F = - kx\], where, k is the spring constant and x is the displacement of the spring from its mean position.

Complete step by step answer:
a) We have according to Hooke’s law; the restoring force is proportional to the displacement of the spring. We can express Hooke’s law as,
\[F = - kx\], where, k is the spring constant and x is the displacement of the spring from its mean position.

The negative sign indicates that the restoring force opposes the applied force. Since the restoring force is proportional to the negative of the displacement, we can draw the graph between spring force and positive displacement of the spring as shown in the figure below,

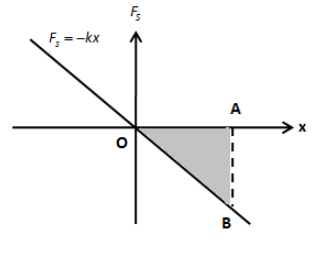
b) The area under the curve of the force is the area of the triangle \[\Delta OAB\]. The area of the above triangle is,
\[A = \dfrac{1}{2}\left( {AB} \right)\left( {OA} \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( { - kx} \right)\left( x \right)\]
\[ \Rightarrow A = - \dfrac{1}{2}k{x^2}\]

The expression on the right hand side of the above equation is the potential energy of the spring due to restoring force. Therefore, we can write,
\[P.E = - \dfrac{1}{2}k{x^2}\]

We know that the restoring force is equal to the applied force on the spring but in the opposite direction. Therefore, the potential energy stored in the spring due to the applied force equals to,
\[\therefore P.E = \dfrac{1}{2}k{x^2}\]

Note:When we displace the spring from its mean position, the work is done on the spring by the spring force. The expression for this work done is the same as the potential energy stored in the spring since the work done is stored in the spring in the form of potential energy. If you determine the change in the potential energy of the spring, you can easily calculate the change in the kinetic energy of the spring since it is the negative of the change in the potential energy.