Question

A dog of mass 5 kg is standing on a flat boat of mass 20 kg, such that it is 10 m away from the shore. The dog then moves 4 m towards the shore and finally halts. Find the final separation between the dog and the shore.
(A) 3.4 m
(B) 6.8 m
(C) 12.6 m
(D) 10 m

Answer 1

Hint: Refer to Newton’s third law of motion. Use the theorem of conservation of momentum to express the center of mass of the system of dog and boat. The position of center of mass of the system does not change.

Formula used:
\[\Rightarrow{R_{CM}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}}\]
Here, \[{x_1}\] is the distance of point 1 from the origin, \[{m_1}\] is the mass of point 1, \[{m_2}\] is the mass of second point, and \[{x_2}\] is the distance of point 2 from the origin.

Complete step by step answer:
According to Newton’s third law of motion, if a body exerts a force on the second body, the second body will also exert an equal amount of force in the opposite direction. In this case, as a dog walks on the boat, in response to this, the boat will also move in the opposite direction.Let x be distance moved by the boat from the shore. The diagrammatic representation of the system of dog and boat can be drawn as below.

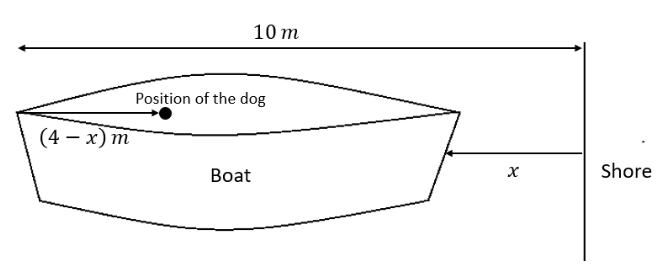
From the above figure, the displacement of the dog with respect to ground is \[\left( {4 - x} \right)\,m\].
The position of the centre of mass of the system of dog and boat is,
\[\Rightarrow{R_{CM}} = \dfrac{{{m_{dog}}{x_1} + {m_{boat}}{x_2}}}{{{m_{dog}} + {m_{boat}}}}\]
Here, \[{x_1}\] is the distance of the dog from the origin, \[{m_{dog}}\] is the mass of dog, \[\Rightarrow{m_{boat}}\] is the mass of boat, and \[{x_2}\] is the distance of boat from the origin.
Let the origin is at the centre of mass of the system.
According to the conservation of momentum, the position of the centre of mass will not change. Therefore, substitute 0 for \[{R_{CM}}\] in the above equation.
\[\Rightarrow0 = \dfrac{{{m_{dog}}{x_1} + {m_{boat}}{x_2}}}{{{m_{dog}} + {m_{boat}}}}\]
\[ \Rightarrow {m_{dog}}{x_1} = - {m_{boat}}{x_2}\]
Since the boat moves in the opposite direction of the movement of the dog, substitute \[ - {x_2}\] for \[{x_2}\] in the above equation.
\[\Rightarrow{m_{dog}}{x_1} = {m_{boat}}{x_2}\]
Substitute 50kg for \[{m_{dog}}\], 20 kg for \[{m_{boat}}\], \[\left( {4 - x} \right)\,m\] for \[\Rightarrow{x_1}\], and x for \[{x_2}\] in the above equation.
\[
\Rightarrow \left( {5\,kg} \right)\left( {4 - x} \right)m = \left( {20\,kg} \right)x \\
\Rightarrow x = 0.8\,m \\
\]
So, the displacement of the dog is,
\[\Rightarrow \left( {4 - x} \right) = \left( {4 - 0.8} \right) = 3.2\,m\]
Therefore, the dog will be at a distance from the shore is,
\[\Rightarrow 10 - 3.2 = 6.8\,m\]

So, the correct answer is option (B).

Note: In this question, the movement of the boat is opposite to the movement of the dog. Therefore, the distance is taken as negative.