Question

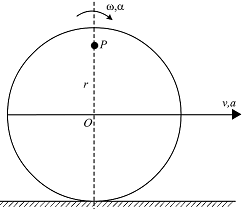
A disc of radius R rolls on a horizontal ground with linear acceleration and angular acceleration α as shown in figure. The magnitude of acceleration of point P at an instant when its linear velocity is v and angular velocity is ω will be:
\[a.\sqrt {{{(a + ra)}^2} + (r{\omega ^2}} {)^2}\]
\[b.\dfrac{{ar}}{R}\]
\[c.\sqrt {{r^2}{a^2} + {r^2}} {\omega ^2}\]
\[d.ra\]
\[\]

Answer 1

Hint: We can separate the acceleration of the particle P into 2 components. One is a radial component and another one a tangential component. The radial component is a component that moves radially outwards from the point O. Tangential components act along the tangential to the circle or perpendicular to the radius.

Complete step by step answer:
There are two components of acceleration at the point P. The first component is in radial direction, which is given by \[r{w^2}\].The second component is in a tangential direction, given by rα. Additionally, we know that every point on the disc possesses a forward acceleration of a. Therefore, we have total forward acceleration as a+ rα
With the information given above, we can get the resultant acceleration of the point P as
\[\sqrt {{{(a + ra)}^2} + (r{\omega ^2}} {)^2}\]
Additional information:
Simple harmonic motion refers to the projection of uniform circular motion on the diameter of a circle inside which circular motion arises.
Consider the particle P' is moving about the circumference of the circle with constant speed omega. The radius of the circle xm is the magnitude of the position vector of the particle.
At any point of time, the angular position of P' is where ∅ is the angular position of P' at t=0.
The projection of the particle's position vector on the x axis, \[(\omega xt + \phi )\]gives the location x (t) of particle P.
Thus, we can summarize the projection of the particle on the x- axis as
\[{x_t} = {x_m} + \cos (\omega t + \phi )\]
Now, let us consider the velocity of the projection, we have to differentiate the position vector.
\[{x_t} = {x_m} + \cos (\omega t + \phi )\]
We can differentiate the distance with respect to time.
\[v(t) = \dfrac{{dx(t)}}{{dt}}\]
Let us resolve into two components as sin and cos.
\[{x_t} = {x_m} + \cos (\omega t + \phi )\]
\[vt = - {x_m} + (\sin \omega t + \phi )\]
 This is the required equation of velocity in Simple Harmonic Motion.
\[vt = - {x_m} + (\sin \omega t + \phi )\]
Now, to find the acceleration of particle P
We know,
\[A(t) = \dfrac{{dv(t)}}{{dt}}\]
since acceleration is defined as the rate of change of velocity.
At=xm+2cos wt+ϕ This is the required equation for acceleration in Simple Harmonic Motion.


Note:
The two components of the acceleration of point P should not be confused. Also, both these components need to be added and calculated using the formula to calculate the magnitude of acceleration.