
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods ${{F}_{1}}$ and ${{F}_{2}}$ are available. Food ${{F}_{1}}$ costs Rs.4 per unit food and ${{F}_{2}}$ costs Rs.6 per unit. One unit of food ${{F}_{1}}$ contains 3 units of vitamin A and 4 units of minerals. One unit of food ${{F}_{2}}$ contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for a diet that consists of a mixture of these two foods and also meets the mineral nutritional requirements?
Answer
608.1k+ views
Hint: First tabulate the information given in the question then try to make constraints and an expression of price which we have to minimize. Then plot them and find the corner points and get the value of the least by putting the minimum price expression. After that draw the graph of price expressionless that the found price to know any feasible point there or not and finally get the answer.
Complete step-by-step answer:
In the question, it’s given that a diet is to contain at least 80 units of vitamin A and 100 units of minerals.
Now there are two food available ${{F}_{1}}$ and ${{F}_{2}}$ where food ${{F}_{1}}$ costs Rs.4 per unit food and food ${{F}_{2}}$ costs Rs.6 per unit. We are also given information that one unit of food ${{F}_{1}}$ contains 3 units of vitamin A and 4 units of minerals one unit of food ${{F}_{2}}$ contains 6 units of vitamin A and 3 units of minerals.
So let’s say the diet contains x amount or units of food ${{F}_{1}}$ and y mount or units of food ${{F}_{2}}$ .
Now we can give conditions on x, y that $x\ge 0$and $y\ge 0$ .
Let’s tabulate the given information so we get,
Now as we know that the cost of food ${{F}_{1}}$ is Rs.4 per unit and food ${{F}_{2}}$ is Rs.6 per unit.
So the requirement of vitamin A can be written in terms of x and y as 3x + 6y.
As the minimum amount is written is 80 so it can be expressed as,
$3x+6y\ge 80$
Now for the requirement of minerals it can be represented in terms of x and y as 4x + 3y.
As the minimum amount is written as 100 so it can be expressed as,
$4x+3y\ge 100$
Also the conditions of x, y separately are $x\ge 0$and $y\ge 0$ .
The total cost of diet is 4x + 6y which can be represented as letter z.
Hence we have to minimize z.
So the subject the constraints are,
$\begin{align}
& 3x+6y\ge 80 \\
& 4x+3y\ge 100 \\
& x\ge 0,y\ge 0 \\
\end{align}$
So the feasible region is determined by the constraints given.
Now let’s consider $3x+6y\ge 80$
Take it as 3x + 6y = 80, then for
y = 0,
3x = 80
So, $x=\dfrac{80}{30}$ . Hence $\left( \dfrac{80}{3},0 \right)$
Satisfy the line.
For x = 0,
6y = 80
So, $y=\dfrac{40}{3}$ , Hence $\left( 0,\dfrac{40}{3} \right)$ satisfy the line.
Now let’s consider $4x+3y\ge 100$
Take it as 4x + 3y = 100, then for y = 0
4x = 100
So, x = 25, hence (25, 0) satisfy the line.
For x = 0,
3y = 100
So, $y=\dfrac{100}{3}$. Hence $\left( 0,\dfrac{100}{3} \right)$ satisfies the line.
Now take both 3x + 6y = 80 and 4x + 3y = 100 and solve it simultaneously.
So, 4x + 3y = 100, hence 3y = 100 – 4x.
So instead of 3y we will substitute 100 – 4x in equation 3x + 6y = 80 so we get,
3x + 2 (100 – 4x) = 80
On further simplifying we get,
3x + 200 – 8x = 80
Now subtracting 80 on both sides we get,
120 – 5x = 0
Which can be written as 5x = 120
So the value of x = 24
Now as we know the value of x is 24 so by substituting it in 3y = 100 – 4x we get,
$3y=100-4\times 24$
So, 3y = 4
$\therefore y=\dfrac{4}{3}$
Hence the point is $\left( 24,\dfrac{4}{3} \right)$
Now drawing all these in graph paper
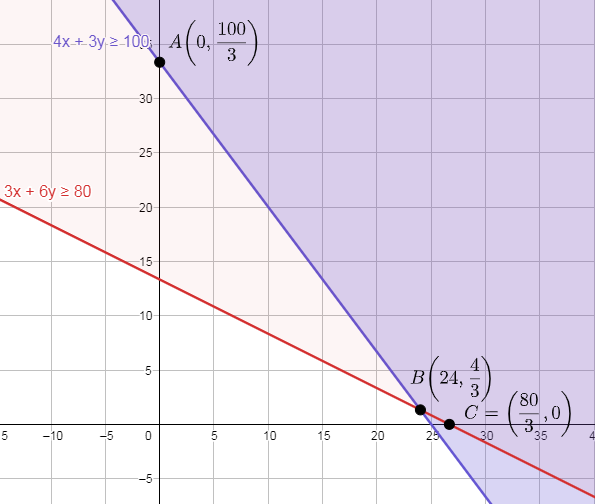
So now let’s assume point A as $\left( 0,\dfrac{100}{3} \right)$ B as $\left( 24,\dfrac{4}{3} \right)$ and C as $\left( \dfrac{80}{3},0 \right)$ .
These points are the corner points of the graph.
So at the point $A\left( 0,\dfrac{100}{3} \right)$ .
Value of z = 4x + 6y
$=4\times 0+\dfrac{100}{3}\times 6=200$
For point B the value of z is Rs. 200
So at point B $\left( 24,\dfrac{4}{3} \right)$
Value of z = 4x + 6y
$=4\times 24+6\times \dfrac{4}{3}=104$
For point B the value of z is Rs.104
So at point C $\left( \dfrac{80}{3},0 \right)$
Value of z = 4x + 6y
$=4\times \dfrac{80}{3}+6\times 0=\dfrac{320}{3}$
For point C the value of z is Rs.$\dfrac{320}{3}$
So, Rs.104 can be or cannot be the minimum value.
For this we need to graph inequality 4x + 6y < 104.
Let’s take equation as 4x +6y = 104
For x = 0
6y = 104
So, $y=\dfrac{52}{3}$ . Hence the point $\left( 0,\dfrac{52}{3} \right)$ satisfies the line.
For y = 0
4x = 104
So, x = 26. Hence, the point (26, 0) satisfies the line.
Since, there is no point common between feasible region and 4x + 6y < 104
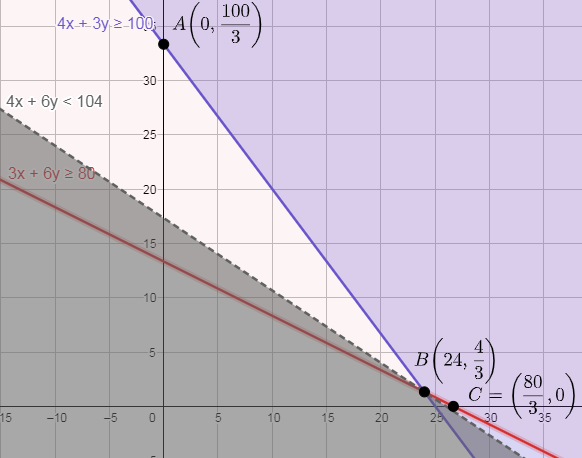
Since, there is no point common between feasible regions and 4x + 6y < 100.
Hence the minimum cost is Rs.104.
Note: Students should be careful while drawing the graph of constraints and inequalities as from the common points or corners answers will come. They should also be careful about any calculation errors.
Complete step-by-step answer:
In the question, it’s given that a diet is to contain at least 80 units of vitamin A and 100 units of minerals.
Now there are two food available ${{F}_{1}}$ and ${{F}_{2}}$ where food ${{F}_{1}}$ costs Rs.4 per unit food and food ${{F}_{2}}$ costs Rs.6 per unit. We are also given information that one unit of food ${{F}_{1}}$ contains 3 units of vitamin A and 4 units of minerals one unit of food ${{F}_{2}}$ contains 6 units of vitamin A and 3 units of minerals.
So let’s say the diet contains x amount or units of food ${{F}_{1}}$ and y mount or units of food ${{F}_{2}}$ .
Now we can give conditions on x, y that $x\ge 0$and $y\ge 0$ .
Let’s tabulate the given information so we get,
| Vitamin A(units) | Mineral(units) | Cost per unit(Rs) | |
| Food ${{F}_{1}}\left( x \right)$ | 3 | 4 | 4 |
| Food ${{F}_{2}}\left( y \right)$ | 6 | 3 | 6 |
| Requirements | 80 | 100 |
Now as we know that the cost of food ${{F}_{1}}$ is Rs.4 per unit and food ${{F}_{2}}$ is Rs.6 per unit.
So the requirement of vitamin A can be written in terms of x and y as 3x + 6y.
As the minimum amount is written is 80 so it can be expressed as,
$3x+6y\ge 80$
Now for the requirement of minerals it can be represented in terms of x and y as 4x + 3y.
As the minimum amount is written as 100 so it can be expressed as,
$4x+3y\ge 100$
Also the conditions of x, y separately are $x\ge 0$and $y\ge 0$ .
The total cost of diet is 4x + 6y which can be represented as letter z.
Hence we have to minimize z.
So the subject the constraints are,
$\begin{align}
& 3x+6y\ge 80 \\
& 4x+3y\ge 100 \\
& x\ge 0,y\ge 0 \\
\end{align}$
So the feasible region is determined by the constraints given.
Now let’s consider $3x+6y\ge 80$
Take it as 3x + 6y = 80, then for
y = 0,
3x = 80
So, $x=\dfrac{80}{30}$ . Hence $\left( \dfrac{80}{3},0 \right)$
Satisfy the line.
For x = 0,
6y = 80
So, $y=\dfrac{40}{3}$ , Hence $\left( 0,\dfrac{40}{3} \right)$ satisfy the line.
Now let’s consider $4x+3y\ge 100$
Take it as 4x + 3y = 100, then for y = 0
4x = 100
So, x = 25, hence (25, 0) satisfy the line.
For x = 0,
3y = 100
So, $y=\dfrac{100}{3}$. Hence $\left( 0,\dfrac{100}{3} \right)$ satisfies the line.
Now take both 3x + 6y = 80 and 4x + 3y = 100 and solve it simultaneously.
So, 4x + 3y = 100, hence 3y = 100 – 4x.
So instead of 3y we will substitute 100 – 4x in equation 3x + 6y = 80 so we get,
3x + 2 (100 – 4x) = 80
On further simplifying we get,
3x + 200 – 8x = 80
Now subtracting 80 on both sides we get,
120 – 5x = 0
Which can be written as 5x = 120
So the value of x = 24
Now as we know the value of x is 24 so by substituting it in 3y = 100 – 4x we get,
$3y=100-4\times 24$
So, 3y = 4
$\therefore y=\dfrac{4}{3}$
Hence the point is $\left( 24,\dfrac{4}{3} \right)$
Now drawing all these in graph paper

So now let’s assume point A as $\left( 0,\dfrac{100}{3} \right)$ B as $\left( 24,\dfrac{4}{3} \right)$ and C as $\left( \dfrac{80}{3},0 \right)$ .
These points are the corner points of the graph.
So at the point $A\left( 0,\dfrac{100}{3} \right)$ .
Value of z = 4x + 6y
$=4\times 0+\dfrac{100}{3}\times 6=200$
For point B the value of z is Rs. 200
So at point B $\left( 24,\dfrac{4}{3} \right)$
Value of z = 4x + 6y
$=4\times 24+6\times \dfrac{4}{3}=104$
For point B the value of z is Rs.104
So at point C $\left( \dfrac{80}{3},0 \right)$
Value of z = 4x + 6y
$=4\times \dfrac{80}{3}+6\times 0=\dfrac{320}{3}$
For point C the value of z is Rs.$\dfrac{320}{3}$
So, Rs.104 can be or cannot be the minimum value.
For this we need to graph inequality 4x + 6y < 104.
Let’s take equation as 4x +6y = 104
For x = 0
6y = 104
So, $y=\dfrac{52}{3}$ . Hence the point $\left( 0,\dfrac{52}{3} \right)$ satisfies the line.
For y = 0
4x = 104
So, x = 26. Hence, the point (26, 0) satisfies the line.
Since, there is no point common between feasible region and 4x + 6y < 104

Since, there is no point common between feasible regions and 4x + 6y < 100.
Hence the minimum cost is Rs.104.
Note: Students should be careful while drawing the graph of constraints and inequalities as from the common points or corners answers will come. They should also be careful about any calculation errors.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




