Question

A cylindrical vessel of diameter 4 cm is partly filled with water. 300 lead balls are dropped in it. The rise in the water level is 0.8 cm. The diameter of each ball is............
A. 0.8 cm
B. 0.4 cm
C. 0.2 cm
D. 0.5 cm

Answer 1

Hint: We will be using the fact that the volume of water displaced by the lead balls is equal to the volume of lead balls also and therefore the volume of water rise in the cylinder is equal to the total volume of 300 lead balls. Finally, we will use the fact that volume of sphere is $\dfrac{4}{3}\pi {{r}^{3}}$ and that of a cylinder is $\pi {{R}^{2}}h$ .

Complete step-by-step solution -
Now, we have been given a cylindrical vessel of diameter 4 cm which is partly filled with water and 300 lead balls are dropped in it and the rise in water level is 0.8 cm.

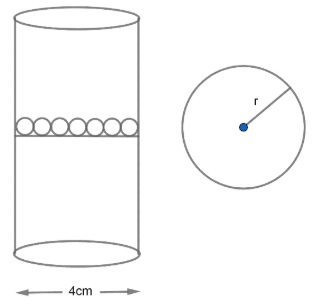
Now, we let the radius of lead ball = r cm
Now, we know that the volume of sphere with radius $r=\dfrac{4}{3}\pi {{r}^{3}}$ cubic units.
So, we have the volume of one lead ball $=\dfrac{4}{3}\pi {{r}^{3}}$
Now, we have the volume of 300 lead balls $=300\times \dfrac{4}{3}\pi {{r}^{3}}$
$=400\pi {{r}^{3}}$
Now, we know that the volume of water displaced by 300 balls is equal to the volume of 300 balls. Also, we have the height of the water rise in the cylinder as 0.8 cm.
So, we have,
Volume of water rise in cylinder = Volume of all 300 lead balls
$\begin{align}
  & \pi {{\left( \dfrac{4}{2} \right)}^{2}}\times 0.8=400\pi {{r}^{3}} \\
 & \pi {{\left( 2 \right)}^{2}}\times 0.8=400\pi {{r}^{3}} \\
 & 4\pi \times 0.8=400\pi {{r}^{3}} \\
 & 0.8=100{{r}^{3}} \\
 & \dfrac{8}{1000}={{r}^{3}} \\
 & r=\sqrt[3]{\dfrac{8}{1000}} \\
 & r=\dfrac{2}{10} \\
 & r=0.2\ cm \\
\end{align}$
 Now, we know that the diameter of ball $=2\times r$
$\begin{align}
  & =2\times 0.2 \\
 & =0.4\ cm \\
\end{align}$
Hence, the correct option is B.

Note: It is important to note that we have used a fact that the volume of water displaced by a lead ball is equal to the volume of the ball. So, we have the volume of water rise in the cylinder equal to the volume of 300 lead balls.