Question

A cylinder of radius $ 12cm $ contains water up to the height of $ 20cm $ . A spherical iron ball is dropped into the cylinder and thus water level is raised by $ 6.75cm $ . What is the radius of the ball?

Answer 1

Hint: For answering this question we will use the given information A cylinder of radius $ 12cm $ contains water up to the height of $ 20cm $. The aspherical iron ball is dropped into the cylinder and thus water level is raised by $ 6.75cm $. So we can say that when the spherical iron ball is dropped into the cylinder the volume of the water raised will be equal to the volume of the spherical iron ball stated from Archimedes’ principle.

Complete step by step answer:
Now considering the question we have a cylinder of radius $ 12cm $ contains water up to the height of $ 20cm $. Aspherical iron ball is dropped into the cylinder and thus water level is raised by $ 6.75cm $.

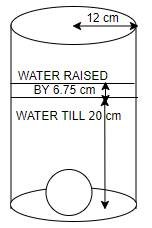
From the concept of Archimedes’ principle, we can state that the volume of the water raised in the cylinder will be equal to the volume of the spherical iron ball dropped.
The volume of the spherical iron ball is given by the formulae $ \dfrac{4}{3}\pi {{r}^{3}} $ .
Let us assume that the radius of the spherical iron ball will be $ {{r}_{1}} $ .
The volume of the cylinder is given by the formulae $ \pi {{r}^{2}}h $ .
Initially the volume of water present in the cylinder is $ \pi {{\left( 12 \right)}^{2}}\left( 20 \right) $ because the radius of the cylinder is given as $ 12cm $ and the height of the water in the cylinder is given as $ 20cm $ .
After dropping the spherical iron ball the height of the water is raised by $ 6.75cm $ . Hence the volume of the water present in the cylinder after this we will have $ \pi {{\left( 12 \right)}^{2}}\left( 12+6.75 \right) $ .
Hence the volume of water raised in the cylinder is $ \pi {{\left( 12 \right)}^{2}}\left( 6.75 \right) $ which will be equal to the volume of the spherical iron ball dropped is $ \dfrac{4}{3}\pi r_{1}^{3} $ . Mathematically it can be given as

$ \begin{align}
  & \dfrac{4}{3}\pi r_{1}^{3}=\pi {{\left( 12 \right)}^{2}}\left( 6.75 \right) \\
 & \Rightarrow \dfrac{4}{3}r_{1}^{3}={{\left( 12 \right)}^{2}}\left( 6.75 \right) \\
 & \Rightarrow r_{1}^{3}={{\left( 12 \right)}^{2}}\left( \dfrac{675}{100} \right)\left( \dfrac{3}{4} \right) \\
\end{align} $
Now by further simplifying this we will have
 $ \begin{align}
  & \Rightarrow r_{1}^{3}={{\left( 12 \right)}^{2}}\left( \dfrac{675}{100} \right)\left( \dfrac{3}{4} \right) \\
 & \Rightarrow r_{1}^{3}=\left( {{3}^{2}}\times {{4}^{2}} \right)\left( {{5}^{2}}\times {{3}^{3}} \right)3\left( \dfrac{1}{{{5}^{2}}\times {{2}^{2}}\times 4} \right) \\
 & \Rightarrow r_{1}^{3}={{3}^{3}}\times {{3}^{3}} \\
 & \Rightarrow {{r}_{1}}=9cm \\
\end{align} $
Therefore we can conclude that the radius of the spherical iron ball is $ 9cm $ .
Note:
 While answering questions of this type we should be sure with our calculations. We should be aware of Archimedes’ principle, when the spherical iron ball is dropped into the cylinder the volume of the water raised will be equal to the volume of the spherical iron ball. The volume of the sphere is given by the formulae $ \dfrac{4}{3}\pi {{r}^{3}} $ . The volume of the cylinder is given by the formulae $ \pi {{r}^{2}}h $ .