Question

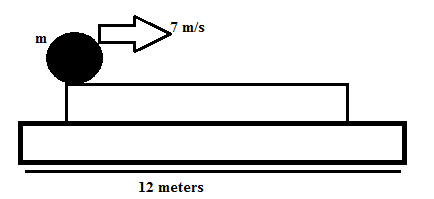
A cylinder of mass m is kept on the edge of a plank of mass 2m and length 12 meter, which in turn is kept on smooth ground. Coefficient of friction between the plank and the cylinder is 0.1. The cylinder is given an impulse, which imparts it a velocity of 7 m/sec but no angular velocity. Find the time after which the cylinder falls off the plank.

Answer 1

Hint: In this question, we need to determine the time at which the cylinder will form the plank such that an impulse has been given to the cylinder which imparts it a velocity of 7 m/sec but no angular velocity. For this, we will use Newton’s laws of motion along with the properties of the friction on a slipping or moving body.

Complete step by step answer:
Given that a Planck is of mass 2m and length 12m. Initially its speed is 7m/s.
Since there are two motions, translational and rotational.
 So for translation motion,
Static friction force, \[{f_S} = \mu N\].
Also, \[N = mg\].
So, \[{f_S} = \mu mg - - - - (i)\].
The free body diagram,

There's is only one horizontal force i.e., \[\;{f_r} = ma - - - - (ii)\]
 Comparing both equations (i) and (ii) we get,
\[a = g\mu \].
(Since velocity is in positive axis and acceleration is in negative axis, so it's also called as retardation)
So,
Now, for Rotational motion,
Rotation about the center will leave only with friction's torque because ‘N’ and ‘mg’ are passing through normal so they'll be cancelled.
\[
  \tau \; = {f_r}\left( R \right) \\
  I\alpha = {\text{ }}{f_r}\left( R \right) \\
 \]
For cylinder:
\[
  \alpha m{R^2} = mg\mu R \\
\Rightarrow \alpha = \;\dfrac{{2G\mu }}{R} \\
   = \dfrac{2}{R} \\
 \]
Now angular velocity is\[\]\[\]
\[
  \omega = {\text{ }}{\omega _0} + \alpha t{\text{ [}}{\omega _0} = 0] \\
\Rightarrow \omega = \alpha t \\
   = \dfrac{{2t}}{R} \\
 \]
For Planck,
\[
  {f_r} = ma \\
\Rightarrow \mu mg = 2ma \\
\Rightarrow a = \dfrac{{\mu g}}{2} \\
   = \dfrac{{0.1 \times 10}}{2} \\
   = 5{\text{ m/}}{{\text{s}}^2} \\
 \]
Now Velocity of cylinder,
\[
  v = u + at \\
   = 7 - 5t \\
 \]

Velocity of Planck is given as:
\[
  v = u + at{\text{ [u = 0]}} \\
\Rightarrow v = at \\
   = 0.5t \\
 \]

When rolling will start,
\[
  v = v - \omega R \\
\Rightarrow 0.5t = \left( {7 - t} \right) - 2t \\
\Rightarrow 0.5t + t + 2t = 7 \\
\Rightarrow 3.5t = 7 \\
\Rightarrow t = 2{\text{ sec}} \\
 \]
At t= 2s pure rolling will start.
Now distance that displacement by center of Mass of cylinder,
\[
  S = ut - \dfrac{1}{2}\mu g{t^2} - \dfrac{1}{2}\left( {\dfrac{{\mu g{t^2}}}{2}} \right) \\
\Rightarrow S = \left( {7 \times 2} \right) - \dfrac{1}{2}\;\left( {0.1 \times 10} \right) \times 4 - \dfrac{1}{2} \times \left( {\dfrac{{0.1 \times 10 \times 4}}{2}} \right) \\
   = 14 - 2 - 1 \\
  S = 11{\text{ }}m \\
 \]
Now after rolling the distance will be given as (12-11) = 1 meter.
Also,
$
  {v_c} - {v_p} = {v_0} - \mu gt - \dfrac{{\mu gt}}{2} \\
   = 7 - 0.1 \times 10 \times 2 - \dfrac{{0.1 \times 10 \times 2}}{2} \\
   = 7 - 2 - 1 \\
   = 4{\text{ m/s}} \\
 $
Hence, by distance-time relation,
$t' = \dfrac{1}{4} = 0.25{\text{ sec}}$
Therefore, the net time in which the cylinder will fall is given as:
$
  t = 2 + 0.5 \\
   = 2.25{\text{ sec}} \\
 $
Hence, the cylinder will fall off the plank after 2.25 seconds.

Note:
Usually, students forget to use the coefficient of friction here with the gravitational force term. A body will start to move only when the static friction which is acting opposite to the direction of applied force has been overcome. Also, a frictional force will always act on the body even when the body is in motion known as dynamic friction as given in the problem.