
A cylinder of mass $m$ and radius $R$ is rolling without slipping on a horizontal surface with angular velocity \[{\omega _0}\]. The velocity of the center of mass of the cylinder is ${\omega _0}R$. The cylinder comes across a step of height $\dfrac{R}{4}$. Then the angular velocity of the cylinder just after the collision is (Assume cylinder remains in contact and no slipping occurs on the edge of the step.)
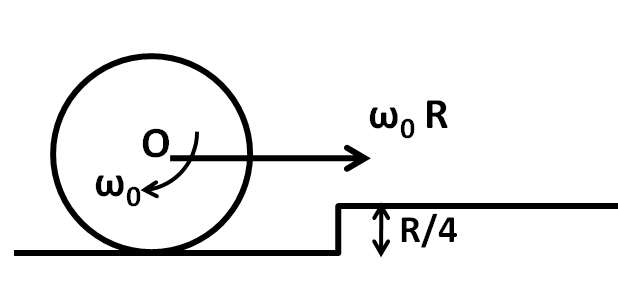
(A) $\dfrac{{5{\omega _0}}}{6}$
(B) ${\omega _0}$
(C) $2{\omega _0}$
(D) $6{\omega _0}$

Answer
542.4k+ views
Hint Hint: To solve this question, we need to use the theorem of conservation of angular momentum. For that, we have to equate the angular momentum of the cylinder about the edge of the step, before and after the collision.
Formula used: The formulae used to solve this question are
(A) $L = I\omega $, here $L$ is the angular momentum, $\omega $ is the angular velocity , and $I$ is the moment of inertia.
(B) $L = mvr$, here $L$ is the angular momentum of an object about a point moving with a velocity of $v$ at a perpendicular distance of $r$ from the point.
Complete step-by-step solution:
The rolling cylinder will interact with the step at the point P as shown in the below figure.
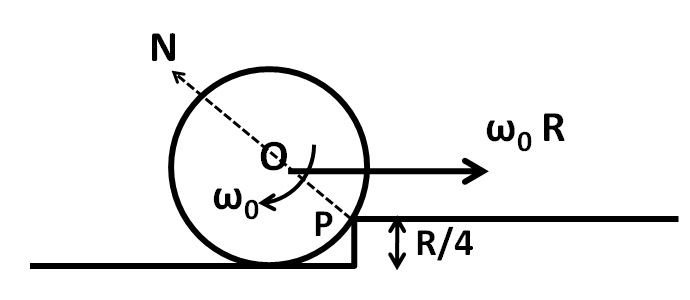
As we can see that a normal force $N$ acts on the cylinder at the point P. Since $N$ passes through the point P, so its torque about the point P is equal to zero. This means that the angular momentum of the cylinder about P is conserved.
Initial angular momentum:
In the above figure, the cylinder is rotating with the angular velocity of \[{\omega _0}\] and it is also translating with a velocity of ${\omega _0}R$ about the point P. So the total initial angular momentum about P is given by
${L_1} = I{\omega _0} + m\left( {{\omega _0}R} \right)r$.........(1)
The perpendicular distance of the velocity vector from the point P from the above figure can be given by
$r = R - \dfrac{R}{4}$
$ \Rightarrow r = \dfrac{{3R}}{4}$..................(2)
Also, we know that the moment of inertia of a cylinder about its natural axis is given by
$I = \dfrac{1}{2}m{R^2}$ …………………..(3)
Putting (2) and (3) in (1) we get
${L_1} = \dfrac{1}{2}m{R^2}{\omega _0} + m\left( {{\omega _0}R} \right)\dfrac{{3R}}{4}$
$ \Rightarrow {L_1} = \dfrac{1}{2}m{R^2}{\omega _0} + \dfrac{3}{4}m{\omega _0}{R^2}$
On simplifying, we get
${L_1} = \dfrac{5}{4}m{R^2}{\omega _0}$ ……..(4)
Final angular momentum:
Let the final angular velocity of the cylinder be $\omega $, as shown in the below figure.
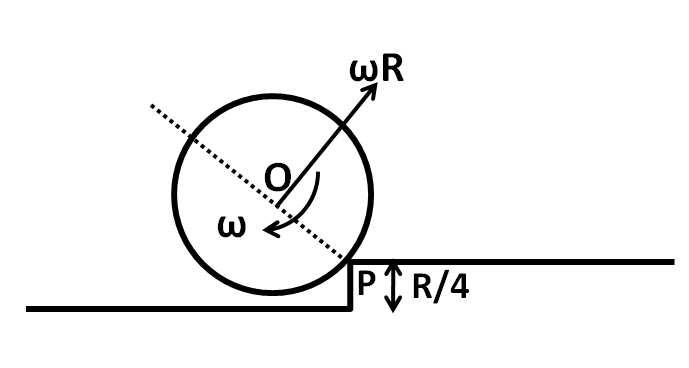
Since it is given that no slipping occurs on the edge, the translational velocity of the centre of mass of the cylinder is given by
$v' = \omega R$ …………..(5)
Since the cylinder is translating with velocity $v$ and rotating about the point P with angular velocity $\omega $, so its final angular momentum about P is given by
${L_2} = I\omega + mv'r$
In this case, the perpendicular distance of P from the velocity vector is equal to the radius, as can be seen in the above figure. So we can put $r = R$ in the above equation to get
${L_2} = I\omega + mv'R$
Putting (3) and (5) in the above equation, we get
${L_2} = \dfrac{1}{2}m{R^2}\omega + m\left( {\omega R} \right)R$
$ \Rightarrow {L_2} = \dfrac{1}{2}m{R^2}\omega + m\omega {R^2}$
On simplifying we get
${L_2} = \dfrac{3}{2}m{R^2}\omega $ …………..(6)
Now, by the conservation of angular momentum, we equate (4) and (6) to get
$\dfrac{5}{4}m{R^2}{\omega _0} = \dfrac{3}{2}m{R^2}\omega $
Cancelling $m{R^2}$ from both the sides, we get
$\dfrac{5}{4}{\omega _0} = \dfrac{3}{2}\omega $
$ \Rightarrow \dfrac{3}{2}\omega = \dfrac{5}{4}{\omega _0}$
Multiplying with $\dfrac{2}{3}$ we finally get
\[\dfrac{2}{3} \times \dfrac{3}{2}\omega = \dfrac{2}{3} \times \dfrac{5}{4}{\omega _0}\]
\[ \Rightarrow \omega = \dfrac{{5{\omega _0}}}{6}\]
Hence, the correct answer is option A.
Note: We can also attempt this question using the concept of instantaneous axis of rotation. The given cylinder will have a pure rotation about the instantaneous axis passing through P and perpendicular to the plane of the cylinder. So its angular momentum about P will be given by $L = I'\omega $, where $I'$ will be the moment of inertia about the instantaneous axis of rotation, which can be obtained by using the parallel axis theorem.
Formula used: The formulae used to solve this question are
(A) $L = I\omega $, here $L$ is the angular momentum, $\omega $ is the angular velocity , and $I$ is the moment of inertia.
(B) $L = mvr$, here $L$ is the angular momentum of an object about a point moving with a velocity of $v$ at a perpendicular distance of $r$ from the point.
Complete step-by-step solution:
The rolling cylinder will interact with the step at the point P as shown in the below figure.

As we can see that a normal force $N$ acts on the cylinder at the point P. Since $N$ passes through the point P, so its torque about the point P is equal to zero. This means that the angular momentum of the cylinder about P is conserved.
Initial angular momentum:
In the above figure, the cylinder is rotating with the angular velocity of \[{\omega _0}\] and it is also translating with a velocity of ${\omega _0}R$ about the point P. So the total initial angular momentum about P is given by
${L_1} = I{\omega _0} + m\left( {{\omega _0}R} \right)r$.........(1)
The perpendicular distance of the velocity vector from the point P from the above figure can be given by
$r = R - \dfrac{R}{4}$
$ \Rightarrow r = \dfrac{{3R}}{4}$..................(2)
Also, we know that the moment of inertia of a cylinder about its natural axis is given by
$I = \dfrac{1}{2}m{R^2}$ …………………..(3)
Putting (2) and (3) in (1) we get
${L_1} = \dfrac{1}{2}m{R^2}{\omega _0} + m\left( {{\omega _0}R} \right)\dfrac{{3R}}{4}$
$ \Rightarrow {L_1} = \dfrac{1}{2}m{R^2}{\omega _0} + \dfrac{3}{4}m{\omega _0}{R^2}$
On simplifying, we get
${L_1} = \dfrac{5}{4}m{R^2}{\omega _0}$ ……..(4)
Final angular momentum:
Let the final angular velocity of the cylinder be $\omega $, as shown in the below figure.

Since it is given that no slipping occurs on the edge, the translational velocity of the centre of mass of the cylinder is given by
$v' = \omega R$ …………..(5)
Since the cylinder is translating with velocity $v$ and rotating about the point P with angular velocity $\omega $, so its final angular momentum about P is given by
${L_2} = I\omega + mv'r$
In this case, the perpendicular distance of P from the velocity vector is equal to the radius, as can be seen in the above figure. So we can put $r = R$ in the above equation to get
${L_2} = I\omega + mv'R$
Putting (3) and (5) in the above equation, we get
${L_2} = \dfrac{1}{2}m{R^2}\omega + m\left( {\omega R} \right)R$
$ \Rightarrow {L_2} = \dfrac{1}{2}m{R^2}\omega + m\omega {R^2}$
On simplifying we get
${L_2} = \dfrac{3}{2}m{R^2}\omega $ …………..(6)
Now, by the conservation of angular momentum, we equate (4) and (6) to get
$\dfrac{5}{4}m{R^2}{\omega _0} = \dfrac{3}{2}m{R^2}\omega $
Cancelling $m{R^2}$ from both the sides, we get
$\dfrac{5}{4}{\omega _0} = \dfrac{3}{2}\omega $
$ \Rightarrow \dfrac{3}{2}\omega = \dfrac{5}{4}{\omega _0}$
Multiplying with $\dfrac{2}{3}$ we finally get
\[\dfrac{2}{3} \times \dfrac{3}{2}\omega = \dfrac{2}{3} \times \dfrac{5}{4}{\omega _0}\]
\[ \Rightarrow \omega = \dfrac{{5{\omega _0}}}{6}\]
Hence, the correct answer is option A.
Note: We can also attempt this question using the concept of instantaneous axis of rotation. The given cylinder will have a pure rotation about the instantaneous axis passing through P and perpendicular to the plane of the cylinder. So its angular momentum about P will be given by $L = I'\omega $, where $I'$ will be the moment of inertia about the instantaneous axis of rotation, which can be obtained by using the parallel axis theorem.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light




