Question

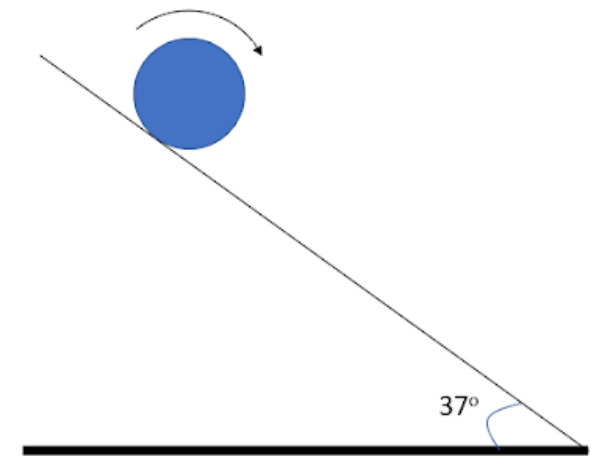
A cylinder having radius 0.4m, initially rotating (at t = 0) with ${{\omega}_{o}}=54rad.{{s}^{-1}}$ is placed on a rough inclined plane with $\theta ={{37}^{o}}$ having friction coefficient $\mu =0.5$. The time taken by the cylinder to start pure rolling is ($g=10m{{s}^{-2}}$)

A. 5.4 s
B. 2.4 s
C. 1.4 s
D. None of these

Answer 1

Hint: First we will find the force of friction and gravity on the cylinder and the torque on the cylinder due to this. After that we will calculate the linear and angular acceleration on the cylinder due to the forces. Finally, we will find the time at which the conditions of pure rolling will be met by the cylinder.

Formula used:
$\begin{align}
  & \tau =I\alpha \\
 & \tau =F.r \\
 & F=ma \\
 & v=\omega r \\
\end{align}$

Complete step-by-step solution:
The cylinder when it touches the plane is purely rotating and has no rectilinear motion. When the plane and the cylinder come in contact with each other, the angular velocity will reduce, and the linear velocity will increase due to the force of friction and gravitational force acting on the body.
The force of friction on the cylinder will be given by
${{F}_{f}}=\mu N=\mu mg\cos \theta $
The force of gravity parallel to the surface of the plane will be
${{F}_{g}}=mg\sin \theta $

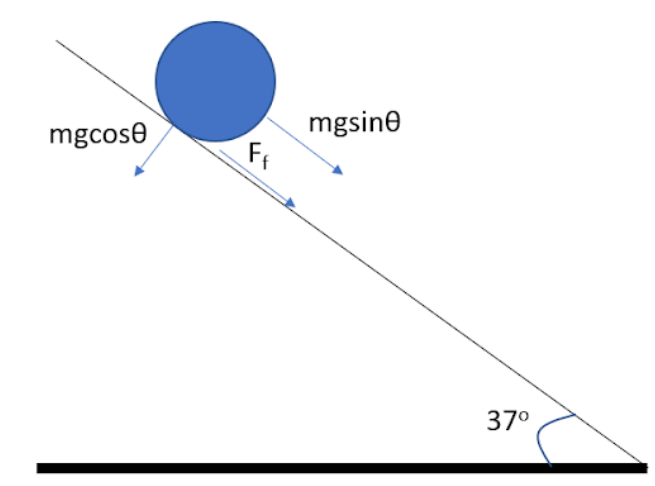
The torque on the cylinder will be given by
$\tau =F.r=\left( \mu mg\cos \theta \times R \right)+\left( mg\sin \theta \times 0 \right)=\mu mgR\cos \theta $
As the force of gravity will act on the centre of the cylinder, there will be no torque due to it.
The angular acceleration due to this torque will be
$\begin{align}
  & \tau =I\alpha \Rightarrow \alpha =\dfrac{\tau }{I} \\
 & I=\dfrac{1}{2}M{{r}^{2}} \\
 & \alpha =\dfrac{\mu mgR\cos \theta }{\dfrac{1}{2}m{{r}^{2}}}=\dfrac{2\mu g\cos \theta }{r} \\
\end{align}$
The linear acceleration on the cylinder due to the force will be
$\begin{align}
  & F=ma\Rightarrow a=\dfrac{F}{m} \\
 & a=\dfrac{\mu mg\cos \theta +mg\sin \theta }{m}=g\left( \mu \cos \theta +\sin \theta \right) \\
\end{align}$
The angular velocity at time t will be given by
$\omega \left( t \right)={{\omega }_{o}}-\alpha t$
The linear velocity at time t will be given by
$v\left( t \right)={{v}_{o}}+at=0+at=at$
There will be pure rolling when
$v=\omega r$
This will happen at time t, for which the following equation is satisfied
$\begin{align}
  & at=\left( {{\omega }_{o}}-\alpha t \right)r=r{{\omega }_{o}}-\alpha rt \\
 & t\left( a+\alpha r \right)=r{{\omega }_{o}}\Rightarrow t=\dfrac{r{{\omega }_{o}}}{a+\alpha r} \\
\end{align}$
$t=\dfrac{r{{\omega }_{o}}}{a+\alpha r}=\dfrac{0.4\times 54}{g\left( \mu \cos \theta +\sin \theta \right)+\dfrac{2\mu g\cos \theta }{r}r}=\dfrac{0.4\times 54}{g\left( \mu \cos \theta +\sin \theta \right)+2\mu g\cos \theta }=\dfrac{0.4\times 54}{g\left( 3\mu \cos \theta +\sin \theta \right)}$
$\begin{align}
  & \theta ={{37}^{o}} \\
 & \cos \theta =\dfrac{4}{5} \\
 & \sin \theta =\dfrac{3}{5} \\
\end{align}$
$\begin{align}
  & t=\dfrac{0.4\times 54}{g\left( \mu \cos \theta +\sin \theta \right)+2\mu g\cos \theta }=\dfrac{0.4\times 54}{g\left( 3\mu \cos \theta +\sin \theta \right)} \\
 & \Rightarrow t=\dfrac{0.4\times 54}{10\left( 3\times 0.5\times \dfrac{4}{5}+\dfrac{3}{5} \right)}=\dfrac{21.6}{10\left( 1.2+0.6 \right)}=\dfrac{21.6}{18}=1.2 \\
\end{align}$
Hence, required time is 1.2 seconds. Hence the correct option is D, i.e. None of these.

Note: Take care to account for the gravitational force which will also increase the linear velocity of the body. There will be no increase in angular velocity due to the gravitational force till the pure rolling starts. When the pure rolling starts there will be an effect of the gravitational force on the angular velocity.