Question

A cue ball moving at 5 ft/s to the right, strikes another billiard ball of equal mass. If the coefficient of restitution between the two is 0.8, find the speed of the cue ball after impact.
A) 1.2 ft/s to the right
B) 0 (it stops completely)
C) 0.5 ft/s to the right
D) -1.2 ft/s to the left

Answer 1

Hint: The problem has to be solved by applying law of conservation of momentum, which states that, “for two or more colliding bodies the total momentum before and after the collision is conserved if no external force acts on them.” The other concept is the coefficient of restitution which is defined as the ratio of relative velocity after collision to the relative collision before collision.

Complete step by step answer:

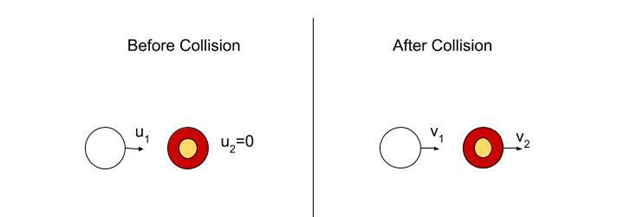
As stated in the problem, the masses of the two balls are the same hence, $m_1 = m_2 = m$.
Applying law of conservation of momentum to the given problem we get,
$m{u_1} + m{u_2} = m{v_1} + m{v_2}$
Assuming, ball 2 to be at rest before collision, i.e. $u_2$= 0. Now, substituting values of $u_2$ & $u_1$ in above equation and also dividing it by m we get,
${v_1} + {v_2} = 5$......................(1)
Now, the formula for coefficient of restitution is given as,
$e = \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}}$
Put e =0.8 in above equation and also put the values of $u_2$ & $u_1$,
$0.8 = \dfrac{{{v_2} - {v_1}}}{{5 - 0}}$
${v_2} - {v_1} = 4$......................(2)
Solving, equations (1) & (2) we get,
${v_1} = 0.5$

Hence, the ball will continue to travel in the same direction with the speed of 0.5 ft/s. Hence, option (C) is the correct choice.

Note: The problems of such type will always have two unknowns to be found. It requires two equations to find solutions for two unknowns. One equation can be obtained by applying the law of conservation of momentum while the other can be obtained by applying the formula for coefficient of restitution. If coeff. of restitution is not provided the chec for any extra condition provided in the question.