Question

A cubical iron block of side 10 cm is floating on mercury in a vessel. What is the height of the block above the mercury level?
Given that the density of the iron is 7.2gm/c.c. and the density of the mercury = 13.6 gm/c.c.

Answer 1

Hint: Archimedes principle can be put to use here. The weight of the body immersed in a fluid is equal to the weight of the fluid displaced by the body. The level by which the cube will be immersed will form an equivalent cube of mercury of the same weight as the entire iron cube.


Complete Step-by-Step solution:
As a body is immersed in a fluid it exerts a force due to its weight, but it also experiences an upward force on it due to the fluid. Therefore a balance is reached when the body displaces fluid weight equal to its own weight. If the body and the fluid have different densities, then it might float or sink. In our case, it is clearly visible that the fluid mercury has a greater density than the object or iron cube. Therefore, it is quite obvious that the iron cube will float above the mercury.

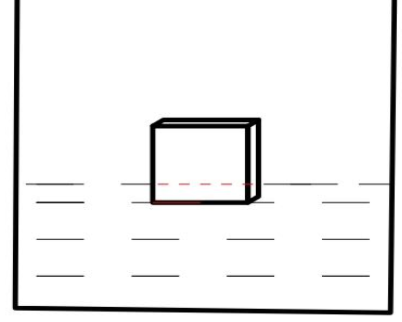
The weight of the mercury displaced is:
$\rho. V. g$
Where mass is just density into volume.
The volume will be equivalent to the immersed cube volume.
Suppose a level x of the cube remains immersed in the mercury then,
$V=A.x$
The weight of the cube is just:
$\rho_{iron} . A . 10cm. g$
Equating the two weights:
$\rho . A.x. g = \rho_{iron} . A . 10cm. g$
Keeping the given values of densities, we get:
$x=\dfrac{7.2}{13.6} . 10cm$
x= 5.294cm
This is the level below the mercury.
Now, in the question it is asked to find the height above the mercury so, it is:
(10-5.294)cm=4.706cm
Therefore our required answer is 4.706 cm approx.

Note: Do not consider the answer complete by just finding the level below the mercury. To avoid this, one can instead use 10-x as the height below the mercury. The x will be the level above the mercury then and one can directly obtain the required answer as the value of x.