Question

A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/ cutting machine and a sprayer. It takes $2$ hours on grinding/ cutting machines and $3$ hours on the sprayer to manufacture a pedestal lamp. It takes $1$ hour on the grinding/ cutting machine and $2$ hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at least for at the most $20$ hours and the grinding/ cutting machine for at the most $12$ hours. The profit from the sale of a lamp is $Rs.5$ and that from a shade is $Rs.3$. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximize his profit?

Answer 1

Hint: In this question use the ISO Profit Method it is an approach to solving a linear programming maximization problem graphically.

Complete Step-by-Step solution:

The number of pedestal lamps to be made is $X$ and the number of wooden shades to be made is $Y$.
Since, pedestal lamps require $2$ hours and wooden shades require $1$ hours of grinding/cutting time. Also, there is a maximum $12$ hours of grinding/ cutting time.
$\therefore 2X + Y \leqslant 12.......1$

Since, pedestal lamps require $3$ hours and wooden shades require $2$ hours for sprayer. Also, there is a maximum $20$ hours for sprayer.
$\therefore 3X + 2Y \leqslant 20.....2$

Since, the count of objects can’t be negative.
$\therefore X \geqslant 0,Y \geqslant 0....3$
We have to maximize the profit of the industry.
Hence, profit on pedestal lamps is $5Rs$ and on wooden shades is $3Rs$
So, objective function is $Z = 5X + 3Y$
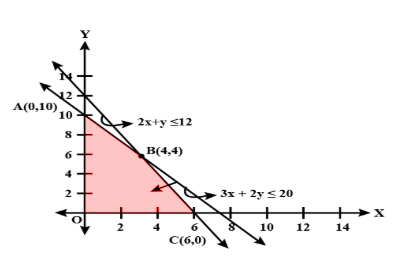
Plotting all the constraints given by equation $1,2,3$ we got the feasible region as shown in the image .
Corner points Value of $Z = 5X + 3Y$
$A\left( {0,10} \right)$ $30$
$B\left( {4,4} \right)$ $32$(maximum)
$C\left( {6,0} \right)$ $30$
Hence , industry should produce $4$ pedestal lamps and $4$ wooden shades in a day to maximize his profit. Also, maximum profit will be $32Rs$.

Note: In such questions ISO Profit Method is applied and this method involves certain steps like
Step $1:$ Draw the half planes of all constraints.
Step $2:$ shade the intersection part which is the feasible region.
Step $3:$ Since the objective function is $Z = ax + by$, draw a dotted line for the equation $ax + by = k$, where $k$ is constant.
Step $4:$ To maximize $Z$ draw a line parallel to $ax + by = k $ and farthest from the origin.
Last step is to find the point in step $4$.