Question

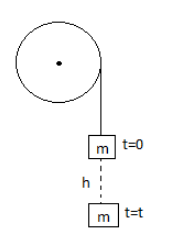
A cord is wound around the circumference of the wheel of radius ‘r’. The axis of the wheel is horizontal and the moment of inertia about it is ‘I’. The weight ‘mg’ is attached to the end of the cord and falls from rest. After falling through a distance ‘h’, the angular velocity of the wheel will be
(A) \[{\left[ {mgh} \right]^{\dfrac{1}{2}}}\]
(B) \[{\left[ {\dfrac{{mgh}}{{I + 2m{r^2}}}} \right]^{\dfrac{1}{2}}}\]
(C) \[{\left[ {\dfrac{{2mgh}}{{I + m{r^2}}}} \right]^{\dfrac{1}{2}}}\]
(D) \[{\left[ {\dfrac{{mgh}}{{I + m{r^2}}}} \right]^{\dfrac{1}{2}}}\]

Answer 1

Hint: In this question, we need to determine the angular velocity of the wheel such that it falls through a distance of ‘h’. For this, we will use the relation between the potential energy and the kinetic energy of the translational body.

Complete step by step answer:
The radius of the wheel is ‘r’ and the moment of inertia of the wheel is ‘I’.
Since, the weight which was attached to the cord initially was at rest, hence its initial velocity will be zero; hence its kinetic energy will also be zero.
Hence its potential energy initially at rest will be \[P.E = mgh - - (i)\]

Now, we know that if the body falls from the rest; then it will gain velocity so its potential energy will converted into the kinetic energy which is due to the kinetic energy of rotation of the wheel and the kinetic energy of translation of the cord; hence this can be written as
\[P.E = K.{E_{translation}} + K.{E_{rotation}} - - (ii)\]
Hence we can write equation (ii) as
\[
\Rightarrow P.E = K.{E_{translation}} + K.{E_{rotation}} \\
\Rightarrow mgh = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}I{\omega ^2} - - (iii) \\
\]
Since the wheel is in rolling motion whose radius is R, hence its velocity can be written as
\[v = \omega R\]
Now substitute the value of velocity in equation (iii), we get
\[
\Rightarrow mgh = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}I{\omega ^2} \\
\Rightarrow mgh = \dfrac{1}{2}m{\left( {\omega R} \right)^2} + \dfrac{1}{2}I{\omega ^2} \\
\Rightarrow\dfrac{1}{2}{\omega ^2}\left( {m{R^2} + I} \right) = mgh \\
\Rightarrow{\omega ^2} = \dfrac{{2mgh}}{{\left( {m{R^2} + I} \right)}} \\
\therefore\omega = \sqrt {\dfrac{{2mgh}}{{\left( {m{R^2} + I} \right)}}} \\
\]
Hence, the angular velocity of the wheel will be \[\omega = \sqrt {\dfrac{{2mgh}}{{\left( {m{R^2} + I} \right)}}} \]
Hence,option C is the correct answer.

Note: It should be noted here that the kinetic energy of the translational rotating body is due to the sum of the rotational kinetic energy and the translational kinetic energy.