
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profit from crops A and B per hectare are estimated as Rs. 10,500 and Rs. 9000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximise the profit?
From LPP from the above and solve it graphically. Do you agree with the message that the protection of the wildlife is utmost necessary to preserve the balance in the environment?
Answer
608.7k+ views
Hint: Star by representing each condition given in the question in the form of mathematical equations and inequalities. After you get all the equations, draw a representative graph and check where all the necessary conditions are being satisfied and you are getting maximum profit.
Complete step by step answer:
To start with the solution, we let the hectare of land allotted to A be x hectares and the hectares of land allotted to B be y hectares.
We know that the net profit is the sum of the total profits, which can be mathematically written as:
Net profit = 10500x + 9000y ………………(i)
The equation of profit is our objective expression.
The constraint on the volume of herbicide used can be written in the form of inequality as
$20\times x+10\times y\le 800.................(ii)$
The other inequality we can get is for the total hectares of land that is to be used.
$x+y\le 50.............(iii)$
And two basic equations are $x\ge 0\text{ and y}\ge \text{0}$ .
So representing all the equations on graph, we get
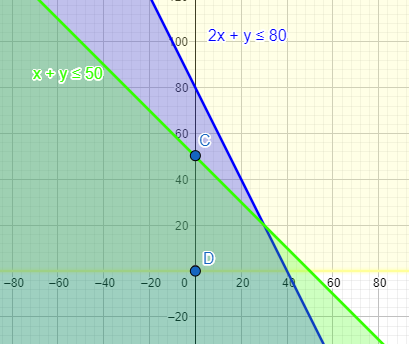
Therefore the objective equations are maximum and minimum at the boundary point of the feasible region.
At (0,0), the profit is equal to 10500x + 9000y = 0
At (40,0), the profit is equal to 10500 $\times $ 40 + 9000y = 420000
At (30,20), the profit is equal to 10500 $\times $ 30 + 9000 $\times $ 20 = 495000
At (0,50), the profit is equal to 10500 $\times $ 0 + 9000 $\times $ 50 = 450000
Therefore, the maximum possible profit is RS. 495000, when crop A is allotted 30 hectares of land and B is allotted 20 hectares of land.
And according to the situation the message that wildlife is more important than money is very apt and important to be followed.
Note: Be sure that the graph is made properly with all the boundary points correctly plotted. Also, use different colours to plot different inequalities as this reduces the chance of making mistakes. If you can’t find the boundary points using the graph then solve all the inequalities taking two inequalities at a time to get the critical points.
Complete step by step answer:
To start with the solution, we let the hectare of land allotted to A be x hectares and the hectares of land allotted to B be y hectares.
We know that the net profit is the sum of the total profits, which can be mathematically written as:
Net profit = 10500x + 9000y ………………(i)
The equation of profit is our objective expression.
The constraint on the volume of herbicide used can be written in the form of inequality as
$20\times x+10\times y\le 800.................(ii)$
The other inequality we can get is for the total hectares of land that is to be used.
$x+y\le 50.............(iii)$
And two basic equations are $x\ge 0\text{ and y}\ge \text{0}$ .
So representing all the equations on graph, we get

Therefore the objective equations are maximum and minimum at the boundary point of the feasible region.
At (0,0), the profit is equal to 10500x + 9000y = 0
At (40,0), the profit is equal to 10500 $\times $ 40 + 9000y = 420000
At (30,20), the profit is equal to 10500 $\times $ 30 + 9000 $\times $ 20 = 495000
At (0,50), the profit is equal to 10500 $\times $ 0 + 9000 $\times $ 50 = 450000
Therefore, the maximum possible profit is RS. 495000, when crop A is allotted 30 hectares of land and B is allotted 20 hectares of land.
And according to the situation the message that wildlife is more important than money is very apt and important to be followed.
Note: Be sure that the graph is made properly with all the boundary points correctly plotted. Also, use different colours to plot different inequalities as this reduces the chance of making mistakes. If you can’t find the boundary points using the graph then solve all the inequalities taking two inequalities at a time to get the critical points.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE

Cutting of the Chinese melon means A The business and class 10 social science CBSE

Show an aquatic food chain using the following organisms class 10 biology CBSE

How is gypsum formed class 10 chemistry CBSE

If the line 3x + 4y 24 0 intersects the xaxis at t-class-10-maths-CBSE

Sugar present in DNA is A Heptose B Hexone C Tetrose class 10 biology CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Indias first jute mill was established in 1854 in A class 10 social science CBSE

Indias first jute mill was established in 1854 in A class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths




