Question

A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs 20 per litre. Also find the cost of the metal sheet used to make the container, if it costs Rs 8 per 100 $c{{m}^{2}}$.

Answer 1

Hint: To solve the above question, we convert the above word problem into mathematical equations. Then we will use the given constraints in the question to arrive at the cost of the metal sheet used to make the container. The formulae are given by –
Volume of frustum = $\dfrac{\pi h}{3}\left( {{R}^{2}}+Rr+{{r}^{2}} \right)$
Surface Area = $\pi (R+r)l+\pi {{R}^{2}}$
Here, r and R are the radii of the bases of the frustum of the cone and l is the slant height of the frustum of the cone

Complete step-by-step answer:
Before beginning to solve the problem, we understand the basics of the frustum of a cone. Basically, a frustum of a cone is a cone obtained after getting cut horizontally across a plane. To explain, a frustum looks like the figure shown below –

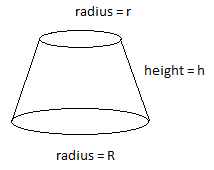
Now, to solve the problems we start to solve the problem by going through the given constraints. We have the frustum of a cone of height is 16 cm with radii of its lower and upper ends as 8 cm and 20 cm. Thus, we have,
h = 16 cm -- (1)
r = 8 cm -- (2)
R = 20 cm -- (3)

We are given that the cost of the milk is Rs 20 per litre. For this, we find the volume of the given frustum in the problem. The formula for the volume of the frustum is $\dfrac{\pi h}{3}\left( {{R}^{2}}+Rr+{{r}^{2}} \right)$. Thus, we substitute the values from (1), (2) and (3) in this formula of the volume. We have,
Volume = $\dfrac{\pi h}{3}\left( {{R}^{2}}+Rr+{{r}^{2}} \right)$
Volume = $\dfrac{\pi (16)}{3}\left( {{20}^{2}}+(20)(8)+{{8}^{2}} \right)$
Volume = $\dfrac{\pi (16)}{3}\left( 624 \right)$
Volume = $3328\pi $ $c{{m}^{3}}$

We know that 1 $c{{m}^{3}}$ = 0.001 litres. Thus, the volume is $3.328\pi $ litres. Thus, given the cost is Rs 20 per litre, we have a total cost as $20\times 3.328\pi $ = Rs 209.104. (for milk)

We are given that the cost of the metal sheet used to make the container is Rs 8 per 100 $c{{m}^{2}}$. To do so, we find the total surface area of frustum to be covered by the metal sheet. We have,
Surface area = $\pi (R+r)l+\pi {{R}^{2}}$ (since, the top having radius r is open, we don’t include it in the area)
Here, l is the slant height given by
l = $\sqrt{{{(R-r)}^{2}}+{{h}^{2}}}$ = $\sqrt{{{(20-8)}^{2}}+{{16}^{2}}}$ = 20 cm
Thus, the surface area is given by

Surface area = $\pi (R+r)l+\pi {{R}^{2}}$ = $\pi (20+8)20+\pi {{20}^{2}}$ = $960\pi \text{ c}{{\text{m}}^{2}}$. Now, the cost is Rs 8 per 100 $c{{m}^{2}}$. Thus, for $960\pi \text{ c}{{\text{m}}^{2}}$, we have the total cost as $\dfrac{8}{100}\times 960\pi $ = Rs 241.274.
Hence, the cost of the metal sheet to cover the frustum of the cone is Rs 241.274.


Note: To calculate the surface area of a figure, we simply find the area of the surfaces of the figure that are to be taken into consideration. In this case, we found the total surface area minus the top area of the frustum (since this was open at the top).

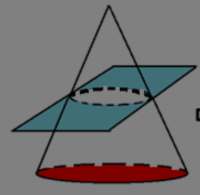
The formulas for the frustum of the cone can be derived by subtracting the formula for the whole cone from the small cone that would be present on the top that would have been cut off to form the frustum as shown on the figure above.