Question

A container open at tops, is the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends, as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of 21 per litre. [Use $$\pi =\dfrac{22}{7}$$]

Answer 1

Hint: In this question it is given that a container open at tops, is the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends, as 8 cm and 20 cm respectively. We have to find the cost of milk which can completely fill the container, at the rate of 21 per liter. So to understand it in better way let us draw the diagram,

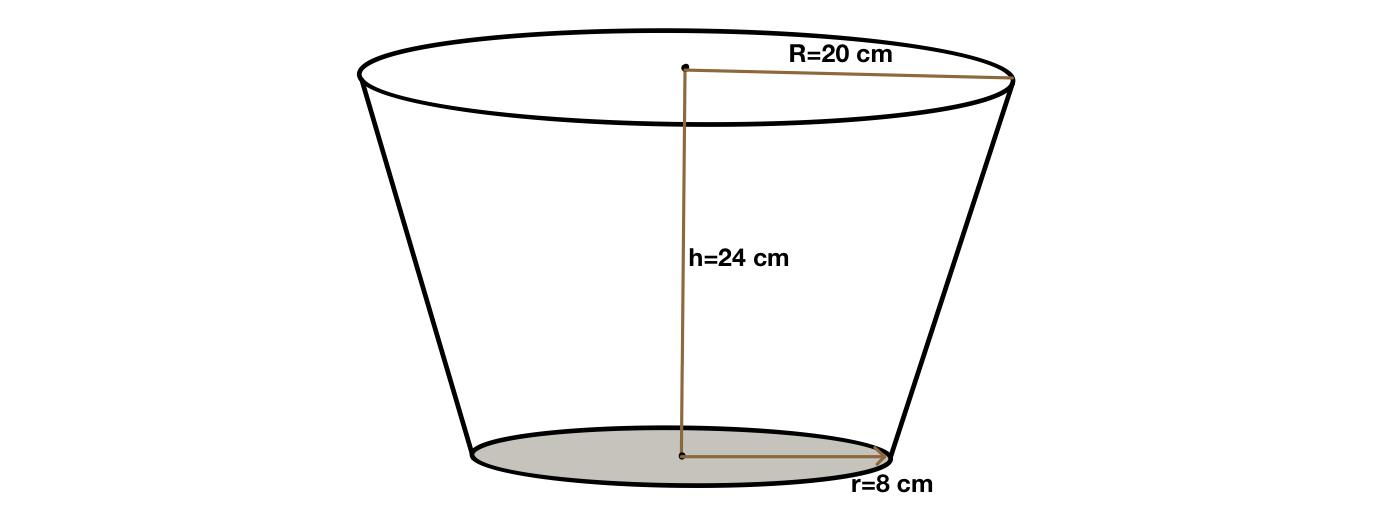
So to find the cost of the milk we first need to find its volume, so to for this we need to know the volume of a frustum of a cone,
$$V=\dfrac{1}{3} \pi h\left( r^{2}+rR+R^{2}\right) $$......(1)
Where,
R= radius of the upper circle
r= radius of the lower circle
h= height of the frustum cone

Complete step-by-step answer:
Given,
Height(h)= 24 cm, upper Radius(R)= 20 cm and lower radius(r)= 8 cm.
Therefore by equation (1) the volume of the frustum cone,
$$V=\dfrac{1}{3} \pi h\left( r^{2}+rR+R^{2}\right) $$
 =$$\dfrac{1}{3} \times \dfrac{22}{7} \times 24\left( 8^{2}+8\times 20+20^{2}\right)\ cm^{3}$$
 =$$\dfrac{1}{3} \times \dfrac{22}{7} \times 24\left( 64+160+400\right)\ cm^{3}$$
 =$$\dfrac{1}{3} \times \dfrac{22}{7} \times 24\times 624\ cm^{3}$$
 =$$\dfrac{1\times 22\times 24\times 624}{3\times 7}\ cm^{3}$$
 =$$\dfrac{329472}{21}\ cm^{3}$$
 =$$15689.1429\ cm^{3}$$
Now as we know that $$1\ cm^{3}=\dfrac{1}{1000} \ litre$$
Therefore, $$15689.1429\ cm^{3}=\dfrac{15689.1429}{1000} \ litre=15.6891\ litre$$(Approx)
As given
The rate of the milk is Rs. 21 per litre.
Thus
Cost of the milk = Volume of the frustum × Cost of milk per litre .
                          =Rs $15.6891\times 21$
                          =Rs 329.4771(Approx)
Therefore the cost of the milk filled in the frustum is Rs 329.4771 .


Note: While solving this type of question you need to know about the volume of a frustum cone which we have already discussed in the hint portion, also when you try to fully fill a three dimensional shape by some liquid or solid then the volume of the shape is always equal to the volume of the poured liquid or solid.