Question

A container is filled with water, accelerating with acceleration $ 10\,m/{s^2} $ , long positive $ X $ -axis on a smooth horizontal surface. The velocity of efflux of water at a point P at the bottom of the tank and near its left most corner is

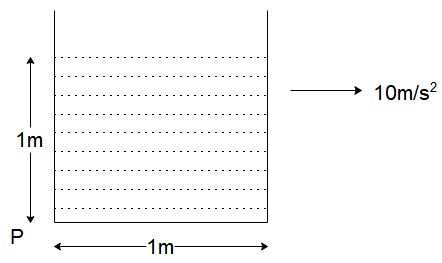
Answer 1

Hint : When the container of the water starts accelerating, the water profile gets tilted away from the acceleration force. The velocity of efflux can be calculated using Bernoulli's theorem.

Formula used: In this solution we will be using the following formula,
Bernoulli’s Equation: $ {P_{atm}} + \rho gh + \dfrac{1}{2}\rho {v^2} = {\text{constant}} $ where $ P $ is the pressure of the water at a certain point, $ {P_{atm}} $ is the atmospheric pressure , $ h $ is the height of the system, and $ v $ is the velocity of the water.

Complete step by step answer:
When the container is filled with water and accelerated, the water profile gets tilted as shown below.

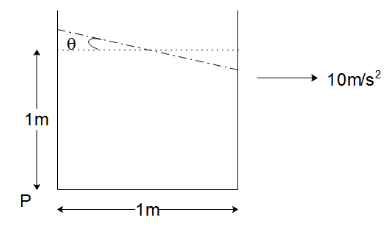
We know that the angle of inclination is calculated as:
 $ \tan \theta = \dfrac{a}{g} $
Since $ a = g = 10\,m/{s^2} $ , the angle of inclination is
 $ \theta = 45^\circ $
Since the length of the container is $ 1\,m $ , the rise in height of the angle will be
 $ h = \dfrac{l}{2}\tan 45^\circ $
 $ \Rightarrow h = \dfrac{l}{2} $
Hence the height of water on the left side will be
 $ h = 1 + \dfrac{1}{2} = \dfrac{3}{2}m $
The velocity of the water can then be calculated using Bernoulli's theorem. Since the water coming out of the container will experience atmospheric pressure too, using Bernoulli’s theorem at the top of the water on the left side and at the bottom of the container of the left side where the water is flowing out, we get
 $ \dfrac{1}{2}\rho {v^2} = \rho gh $
Solving for $ v $ , we get
 $ v = \sqrt {2gh} $
Substituting the values of $ g = 10 $ and $ h = \dfrac{3}{2}m $ , we get
 $ v = \sqrt {2 \times 10 \times \dfrac{3}{2}} $
Which give us
 $ v = \sqrt {30} $
Or $ v = 5.48\,m/s $ .

Note:
The formula for finding the velocity of water as it exits the fluid is also known as Torricelli’s theorem. While using the height to find the velocity of water, we must take into account the change in height of water due to its acceleration.