Question

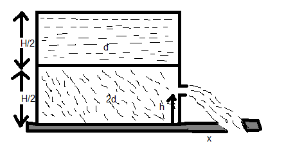
A contain of large uniform cross-sectional area $ A $ resting on a horizontal surface, holds, two immiscible, non-viscous and incompressible liquids of density $ d $ and $ 2d $ , each of height $ \dfrac{H}{2} $ as shown in figure. The lower density liquid is open to the atmosphere having pressure $ {P_0} $ . A homogeneous solid cylinder of length $ L\left( {L < \dfrac{H}{2}} \right) $ , cross- sectional area $ \dfrac{A}{5} $ is immersed such that it floats with its axis vertical at the liquid-liquid interface with length $ \dfrac{L}{4} $ in the denser liquid. The cylinder is then removed and the original arrangement is restored. A tiny hole of area $ s\left( {s < < A} \right) $ is punched on the vertical side of the container at a height $ h\left( {h < \dfrac{H}{2}} \right) $ . As a result of this, liquid starts flowing out of the hole with a range $ x $ on the horizontal surface. The horizontal distance travelled by the liquid, initially is:

$ \left( A \right)\sqrt {\left( {3H + 4h} \right)h} \\
  \left( B \right)\sqrt {\left( {3h + 4H} \right)h} \\
  \left( C \right)\sqrt {\left( {3H - 4h} \right)h} \\
  \left( D \right)\sqrt {\left( {3h - 4H} \right)h} \\ $

Answer 1

Hint :In order to solve the question, we can use the Bernoulli’s equation directly from which the velocity can be found for the layers of the material, and as velocity depends on the distance and the time, so, the initial displacement $ x $ can be easily found from the velocity relation. The principle is only applicable for isentropic flows when turbulences are small and can be neglected.
The formula used here is Bernoulli’s equation for the liquids
 $ {P_1} + \dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} = {P_2} + \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} $
Where $ \rho $ is fluid density, $ g $ is acceleration due to gravity, $ {P_1} $ is pressure at elevation $ 1 $ , $ {v_1} $ is pressure at elevation $ 1 $ , $ {h_1} $ is height of elevation $ 1 $ , $ {h_2} $ is height of elevation $ 2 $ , $ {P_2} $ is pressure at elevation $ 2 $ , $ {v_2} $ is velocity at elevation $ 2 $

Complete Step By Step Answer:
Let us consider that the density of the cylinder is $ \rho $
For the density displacement $ d $ , volume is given as
 $ {V_d} = \dfrac{A}{5} \times \dfrac{{3L}}{4} = \dfrac{{3AL}}{{20}} $
For the density displacement $ 2d $ , volume is given as
 $ {V_{2d}} = \dfrac{A}{5} \times \dfrac{L}{4} = \dfrac{{AL}}{{20}} $
Now, in order to find the initial distance travelled, we apply the Bernoulli’s equation here which is given as
 $ {P_0} + \dfrac{H}{2}dg + \left( {\dfrac{H}{2} - h} \right) \times 2dg = \dfrac{1}{2} \times 2d \times {v^2} + {P_0} $
Further solving, we get,
$ \Rightarrow \dfrac{3}{2}Hdg - 2hdg = d{v^2} \\
   \Rightarrow \dfrac{g}{2}\left( {3H - 4h} \right) = {v^2} \\ $
Now as we know, that
 $ t = \sqrt {\dfrac{{2h}}{g}} $ and $ x = vt $
Using these two relations, we get
 $ x = \sqrt {\left( {3H - 4h} \right)h} $
Hence, option $ \left( C \right)\sqrt {\left( {3H - 4h} \right)h} $ is correct.

Note :
Bernoulli’s principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid’s potential energy , the pressure decreases when the flow speed increases and the principle is only applicable for isentropic flows when turbulences are small and can be neglected.