Question

A conical tent is to accommodate 11 persons. Each person must have 4${m^2}$ of the space on the ground and 20${m^3}$ of air to breathe. Find the height of the conical tent. $\left[ {Take,\pi = \dfrac{{22}}{7}} \right]$

Answer 1

Hint- In the question, we have been given the number of persons and areas needed for each person, so we can get the required area of the base of the cone. Also, the volume of air required for a person to breathe is also given, so we can calculate the total volume of the cone as well. Using these 2 given quantities, we can calculate the height of the cone.

Complete step-by-step answer:
According to question,
11 persons are there and each of them require 4${m^2}$ area on the ground,
$\therefore $Total area of the base of the cone required on the ground $ = 11 \times 4{m^2} \Rightarrow 44{m^2}$.
Each of them requires 20${m^3}$ air to breathe,
$\therefore $Total volume of air required for breathing of 11 persons $ = 11 \times 20{m^3} \Rightarrow 220{m^3}$.
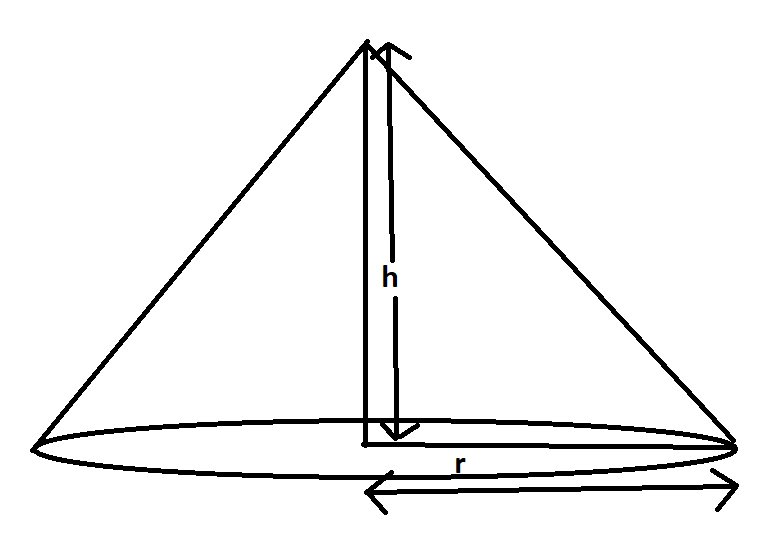
There are 2 unknowns, i.e. radius of base of the cone and height of the cone. Let us consider the radius of the base of the cone is $r$m and the height of the cone is $h$m.
Now, Area of the base of the cone$ = \pi {r^2} = 44$$\Rightarrow {r^2} = \dfrac{{44}}{\pi } \Rightarrow \dfrac{{44}}{{\dfrac{{22}}{7}}} = 14$
$ \Rightarrow r = \sqrt {14} m$
Also, Volume of cone$ = \dfrac{1}{3}\pi {r^2}h = 220 \Rightarrow \dfrac{1}{3} \times \pi \times {\left( {\sqrt {14} } \right)^2} \times h = 220$
$\therefore h = \dfrac{{220 \times 3 \times 7}}{{22 \times 14}} \Rightarrow 15$m
Hence, we obtain the height of the cone $ = 15$m

Note- For solving such questions, we have to calculate the total area occupied and total volume required. After calculating the radius of the base of the cone, then we can calculate the height of the cone using the calculated volume of the cone. We will use base of cone which is circular in shape and volume of cone expression as given below: ${A_{Base}} = \pi {r^2}$ and ${V_{Cone}} = \dfrac{1}{3}\pi {r^2}h$.