Question

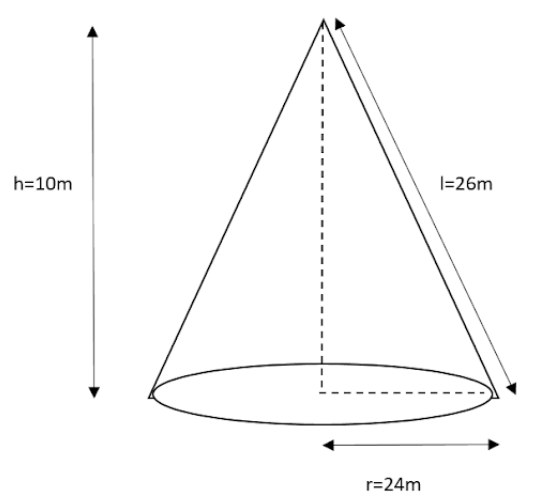
A conical tent is $10m$ high and radius of its base is $24m$. Find
i) Slant height of the tent and
ii) cost of the canvas required to make the tent, if the cost of $1{m^2}$ canvas is 70.

Answer 1

Hint- In order to solve this problem first we will solve first part of it by using the formula of $\text{slant height} = \sqrt {{{\text{(radius)}}^2} + {{\text{(height)}}^2}} $ further to solve second part first we will calculate the surface area of tent and at last by multiplying it with cost of $1{m^2}$ we will get the required answer.

Complete step-by-step solution -
Given that height of conical tent$(h) = 10m$
Radius of conical tent $(r) = 24m$
i) Let the slant height of the tent be $l$
As we know that slant height of cone is given as
$l = \sqrt {{r^2} + {h^2}} $
Substitute the values of height and radius we have
\[l = \sqrt {{{(24)}^2} + {{(10)}^2}} \\
\Rightarrow l = \sqrt {576 + 100} \\
\Rightarrow l = \sqrt {676} \\
\Rightarrow l = 26 \\ \]
Therefore, the slant height of the tent is 26m.

ii) Here in this question the tent doesn't cover the base, so we find a curved surface area of the tent .
As we know that curved surface area of cone is given as
Curved surface area of cone = \[\pi rl\]
Here, \[r\] is the radius of the cone and \[l\] is the slant height of the cone
By substituting the values we have
Curved surface area of tent =
\[ (\dfrac{{22}}{7} \times 24 \times 26){m^2} \\
   = \dfrac{{13728}}{7}{m^2} \\ \]
Now, it is given that cost of $1{m^2}$ canvas = \[70Rs.\].
Therefore, cost of \[\dfrac{{13728}}{7}{m^2}\] canvas = \[ \dfrac{{13728}}{7} \times 70 \\ = 137280Rs. \\ \]
Hence, the cost of canvas required to make the tent is \[137280Rs.\].

Note- Curved surface area of the cone is given by \[\pi rl\] where \[r\] is the radius of the cone and \[l\] is the slant height of the cone and we can find the slant height of the cone with the help of height and radius of the cone which is given by $l = \sqrt {{r^2} + {h^2}} $.