Question

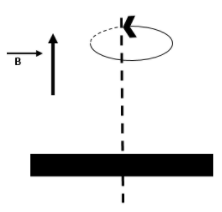
A conducting rod of length 2l is rotating with constant singular, speed about its perpendicular bisector. A uniform magnetic field \[\overrightarrow{B}\] exists parallel to the axis of rotation. The emf Induced between two ends of the rod is

A) \[Bw{{l}^{2}}\]
B) \[\dfrac{1}{2}Bw{{l}^{2}}\]
C) \[\dfrac{1}{8}Bw{{l}^{2}}\]
D) Zero

Answer 1

Hint: Since, a conducting rod of length 2l is rotating with constant angular speed w about its \[\bot ar\] bisector and a uniform magnetic field \[\overrightarrow{B}\] exists \[\parallel r\] to the axis of rotation. So, we used the formula of induced emf due to rotation.

Complete answer:
Let us assume a small element dx of a distance x from the rod rotating with an angular speed w about its perpendicular bisectors. Due to the rotation, the emf induced in the small amount element is given by
\[de=Bwxdx\]
Where de = induced emf in the small element
Since, the rod is rotating. So the emf induced between the centre of the rod and one of its side is given by \[de=\int_{0}^{1}{aw}dx\]
On integrating both sides, we get
\[e=Bw\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{l}\]
\[e=Bw\left[ \dfrac{{{1}^{2}}-{{0}^{2}}}{2} \right] \]
\[e=\dfrac{1}{2}Bw{{l}^{2}} \]
From the fig. \[AO=OB=l\]
So, the potential at rod OA \[{{V}_{a}}-{{V}_{0}}=\dfrac{1}{2}Bw{{l}^{2}}\text{ }\left( 1 \right)\]
And the potential at rod OB
\[{{V}_{B}}-{{V}_{0}}=\dfrac{1}{2}Bw{{l}^{2}}\text{ }\left( 2 \right)\]
Subtracting equation 2 from 1 we get
\[{{V}_{A}}-{{V}_{B}}=0\]

Hence, the correct option is D.

Note:
Be careful while calculating the formula induced emf \[e=\dfrac{1}{2}Bw{{l}^{2}}\] and a rod of length 2l is rotating about its bisector. So its length from the centre is taken to be l and calculate the potential on each side of the rod. Use the value provided exactly at the same time.