
A compound ${M_p}{X_q}$ has cubic-close packing (c.c.p) arrangement of X. Its unit-cell structure is shown below. The empirical formula of the compound is:
A) $MX$
B) $M{X_2}$
C) ${M_2}X$
D) ${M_5}{X_{14}}$

Answer
588.6k+ views
Hint: Count the number of M atoms and X atoms at different positions in the given structure of the unit-cell. To answer this question, you should know the contribution of an atom per unit cell, when the atoms are located at the corners, face-centre, and the edge-centre.
Complete step by step answer:
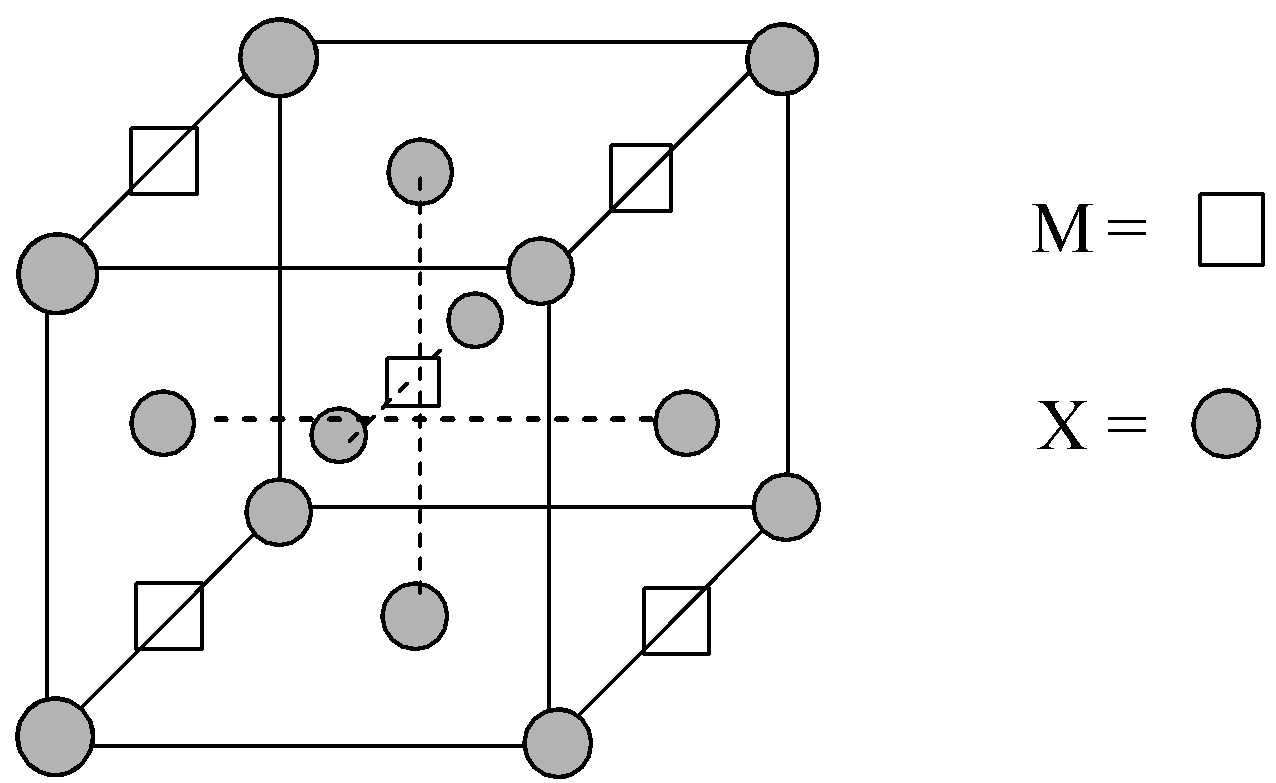
Given structure of the unit cell of the compound ${M_p}{X_q}$:
Now, let us understand the positions of X atoms:
Number of X atoms located at the corners = 8,
Number of X atoms located at the face-centres = 6
And, contribution of an atom located at the corner in a unit cell = $\dfrac{1}{8}$ per unit cell.
Contribution of an atom located at the face-centre in a unit cell = $\dfrac{1}{2}$ per unit cell.
Thus, total number of X atoms in the unit cell = ${\text{8 corner atoms }} \times \dfrac{1}{8}{\text{ atom per unit cell + 6 face - centred atoms }} \times {\text{ }}\dfrac{1}{2}{\text{ atom per unit cell }}$
$\therefore $ Total number of X atoms = $1 + 3 = 4{\text{ atoms}}$
Now, there are four M atoms located at the edge-centres and one atom is located at the body centre of the unit cell.
Contribution of an atom located at the edge centre in a unit-cell = $\dfrac{1}{4}$ per unit cell.
Contribution of an atom located at the body-centre in a unit-cell = 1 per unit cell.
Thus, total number of M atoms in the unit cell = ${\text{4 edge - centred atoms }} \times {\text{ }}\dfrac{1}{4}{\text{ atom per unit cell + 1 body - centred atom }} \times {\text{ 1 atom per unit cell}}$
$\therefore $ Total number of M atoms = $1 + 1 = 2{\text{ atoms}}$
So, there are a total two M atoms and four X atoms in the given unit cell structure. Thus, the empirical formula of the compound is ${M_2}{X_4}$ or on simplifying, $M{X_2}$.
So, the correct answer is “Option B”.
Note: Cubic close packed (ccp) unit cell or face-centred cubic (fcc) unit cell are the same unit cells but two different names. A face-centred unit cell contains atoms at all the corners and at the centre of all the faces of the cubic unit cell. A key point to note is that each atom located at the face centre is shared between two adjacent unit cells and hence only $\dfrac{1}{2}$ of each atom belongs to the unit cell.
Complete step by step answer:
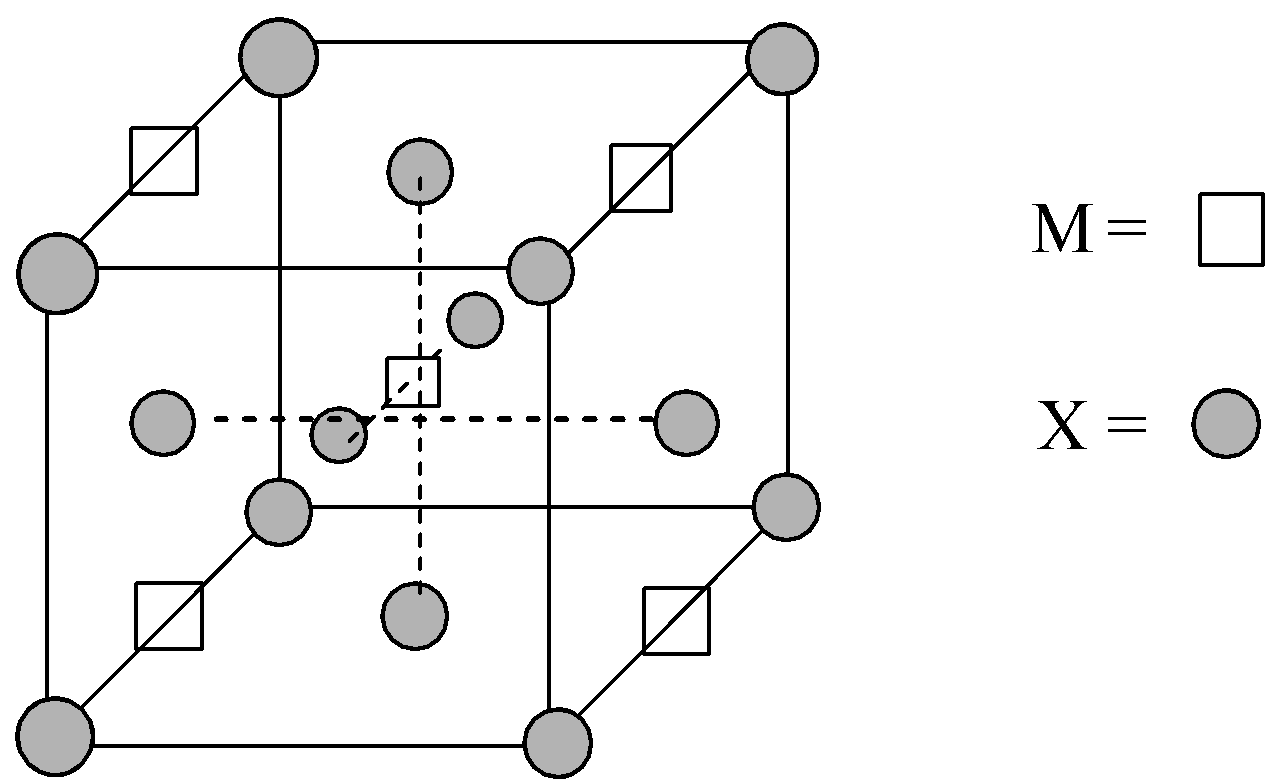
Given structure of the unit cell of the compound ${M_p}{X_q}$:

Now, let us understand the positions of X atoms:
Number of X atoms located at the corners = 8,
Number of X atoms located at the face-centres = 6
And, contribution of an atom located at the corner in a unit cell = $\dfrac{1}{8}$ per unit cell.
Contribution of an atom located at the face-centre in a unit cell = $\dfrac{1}{2}$ per unit cell.
Thus, total number of X atoms in the unit cell = ${\text{8 corner atoms }} \times \dfrac{1}{8}{\text{ atom per unit cell + 6 face - centred atoms }} \times {\text{ }}\dfrac{1}{2}{\text{ atom per unit cell }}$
$\therefore $ Total number of X atoms = $1 + 3 = 4{\text{ atoms}}$
Now, there are four M atoms located at the edge-centres and one atom is located at the body centre of the unit cell.
Contribution of an atom located at the edge centre in a unit-cell = $\dfrac{1}{4}$ per unit cell.
Contribution of an atom located at the body-centre in a unit-cell = 1 per unit cell.
Thus, total number of M atoms in the unit cell = ${\text{4 edge - centred atoms }} \times {\text{ }}\dfrac{1}{4}{\text{ atom per unit cell + 1 body - centred atom }} \times {\text{ 1 atom per unit cell}}$
$\therefore $ Total number of M atoms = $1 + 1 = 2{\text{ atoms}}$
So, there are a total two M atoms and four X atoms in the given unit cell structure. Thus, the empirical formula of the compound is ${M_2}{X_4}$ or on simplifying, $M{X_2}$.
So, the correct answer is “Option B”.
Note: Cubic close packed (ccp) unit cell or face-centred cubic (fcc) unit cell are the same unit cells but two different names. A face-centred unit cell contains atoms at all the corners and at the centre of all the faces of the cubic unit cell. A key point to note is that each atom located at the face centre is shared between two adjacent unit cells and hence only $\dfrac{1}{2}$ of each atom belongs to the unit cell.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Give 10 examples of unisexual and bisexual flowers

Give simple chemical tests to distinguish between the class 12 chemistry CBSE

Define Vant Hoff factor How is it related to the degree class 12 chemistry CBSE




