Question

A coin is sliding down on a smooth hemi-spherical surface of radius R. The height from the bottom, where it loose contact with the surface is
A. $\dfrac{R}{3}$
B. $\dfrac{2R}{3}$
C. $\dfrac{3R}{4}$
D. $\dfrac{4R}{5}$

Answer 1

Hint: As a first step we could depict the given conditions in a neat figure. Consider a point at height h and we know that change in potential energy when the coin slides from height R to h is transferred to its kinetic energy. Now on applying the law of conservation of energy, we could get its velocity. Now balance the forces along the direction of normal force and we know that normal force is zero for the point at which the coin detaches. Now, by doing necessary substitutions we could get the answer.

Complete step-by-step answer:
In the question, we are given a coin that is sliding down a smooth hemispherical surface of radius R. Smooth surface here clearly indicates the absence of friction on the surface. Using the given information, we are asked to find the height from the bottom at which the coin loses contact with hemispherical surfaces.

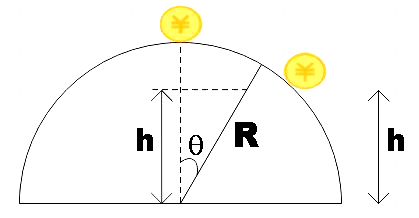
Situation is as depicted in the above diagram.
By law of conservation of energy, we know that the change in potential energy of the coin on sliding from a height R to height h is transferred to kinetic energy. That is, mathematically,
$\dfrac{1}{2}m{{v}^{2}}=mgR-mgh$
But from the figure, we can express height h as,
$h=R\cos \theta $
$\Rightarrow \dfrac{1}{2}m{{v}^{2}}=mgR-mgR\cos \theta $
$\Rightarrow {{v}^{2}}=2gR\left( 1-\cos \theta \right)$ ……………………………………… (1)
Also, when the coin detaches from the surface the normal force on it will be zero. Let us look at the free body diagram.

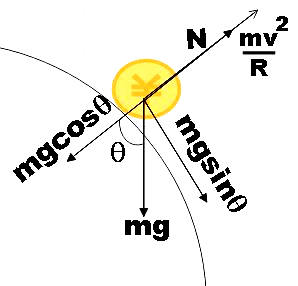
Now let us balance the forces acting along the direction of normal,
$N=mg\cos \theta -\dfrac{m{{v}^{2}}}{R}$
But when the coin detaches from the surface, the normal force is known to be zero. So,
$mg\cos \theta =\dfrac{m{{v}^{2}}}{R}$
$\Rightarrow g\cos \theta =\dfrac{{{v}^{2}}}{R}$
Substituting (1),
$g\cos \theta =\dfrac{2gR\left( 1-\cos \theta \right)}{R}$
$\Rightarrow \cos \theta =2-2\cos \theta $
$\Rightarrow \cos \theta =\dfrac{2}{3}$ ……………………………….. (2)
From the first figure,
$\cos \theta =\dfrac{h}{R}$ …………………………… (3)
Combining (2) and (3),
$\dfrac{h}{R}=\dfrac{2}{3}$
$\therefore h=\dfrac{2}{3}R$
Therefore, we found that the height from the bottom, where it loses contact with the surface as$\dfrac{2}{3}R$.

So, the correct answer is “Option B”.

Note: Because of the physical structure of the coin, you may worry about the rolling motion of the coin over the surface. However, here in the question we are specifically given that the coin is undergoing sliding motion. Hence, we could take that as an assurance of the absence of rolling motion in the given case.