Question

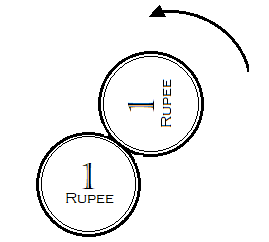
A coin is in a fixed position. Another identical coin is rolled around the edge of the first one. How many complete revolutions will be made by the revolving coin before it reaches its starting point?

(A) $1$
(B) $2$
(C) $3$
(D) $4$

Answer 1

Hint:
If you look at the problem at first glance, the answer that comes to your mind will be that both the circles are identical so they must have the same circumference. And this is the reason why the rotating coin should have a single rotation around the stationary coin. But consider the “rolling motion” of the outer coin on the edge of the fixed coin. This will give you the correct answer.

Complete step by step solution:
Here in this problem, we are given two identical coins. One of the coins is fixed at a position and the other is rolled around the edge of the first one. And we need to find out the number of revolutions completed by the rolling coin when it reaches back to the starting point.

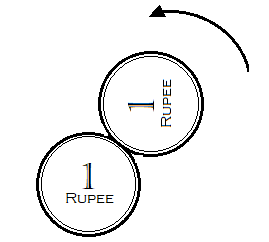
The circumference of both the circles is equal to $2\pi r$, where the radius of these coins is assumed to be ‘r’ and the circumference is defined as the twice of pie $\left( \pi \right)$ times the radius.
But the catch is that in addition to going around the circle is also rolling. Mark any point on the circle as A. Let the circle roll around the inner circle. You will notice that the point itself undergoes a revolution of 360 degrees or $2\pi $ radian. Thus it must travel an additional distance, $l = r \times \theta = 2\pi r$ , which is the product of radius and angle.
So in all, the circle travels a distance $2\pi r + 2\pi r = 4\pi r$.
The distance traveled by a circle in one revolution is its circumference, i.e. $2\pi r$
Therefore, the number of revolutions taken by the rolling coin are $\dfrac{{4\pi r}}{{2\pi r}} = 2$

Hence, the option (B) is the correct answer.

Note:
In general, the rolling condition allows the contact point to rotate around the inner circle at any rate $r$ so long as the two circles themselves are spinning at equal amounts above and below that rate (i.e. at rates $r - s$ and $r + s$ ). The glued together situation is a special case of this with $s = 0$ and the non-rotating inner circle is the case with $s = r$.