Question

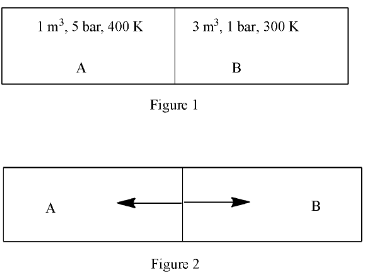
A closed tank has two compartments A and B, both filled with oxygen (assumed to be an ideal gas). The partition separating the two compartments is fixed and is a perfect heat insulator (Figure 1). If the old partition is replaced by a new partition, which can slide and conduct heat does not allow the gas to leak across (Figure 2), the volume (in ${{m}^{3}}$) of the compartment A after the system attains equilibrium is ______________

Answer 1

Hint: We can solve this question by using many formulas like $n=\dfrac{PV}{TR}$, $\dfrac{{{P}_{A}}}{{{T}_{A}}}=\dfrac{{{P}_{B}}}{{{T}_{B}}}$, where P is the pressure, V is the volume, R is the gas constant, T is the temperature, n is the number of moles.

Complete step-by-step answer: So according to Figure 1, in compartment A, the pressure is 5 bar, the volume is 1 ${{m}^{3}}$, and temperature 400 K. This can be written as:
${{P}_{A}}=5$
${{V}_{A}}=1$
${{T}_{1}}=400$
In compartment B, the pressure is 1 bar, the volume is 3 ${{m}^{3}}$, and temperature 400 K. This can be written as:
${{P}_{B}}=1$
${{V}_{B}}=3$
${{T}_{B}}=300$
So, from the given values we can calculate the number of moles for both the compartments by using the formula $n=\dfrac{PV}{TR}$, we get
${{n}_{A}}=\dfrac{\text{ 5 x 1}}{400\text{ x R}}=\dfrac{5}{400R}$
${{n}_{B}}=\dfrac{\text{ 1 x 3}}{300\text{ x R}}=\dfrac{3}{300R}$
The total volume will be = 1 + 3 = 4 ${{m}^{3}}$
In Figure 2, let us assume, the volume of A is x and volume of B is (4 – x).
We know that:
$\dfrac{{{P}_{A}}}{{{T}_{A}}}=\dfrac{{{P}_{B}}}{{{T}_{B}}}$, because it will attain equilibrium.
This can be written as:
$\dfrac{{{n}_{A}}\text{ x R}}{{{V}_{A}}(new)}=\dfrac{{{n}_{B}}\text{ x R}}{{{V}_{B}}(new)}$
Putting, the values in this, we get:
$\dfrac{5}{400(x)}=\dfrac{3}{300(x-4)}$
For solving x, we get:
$5(4-x)=4x$
${{V}_{A}}=x=\dfrac{20}{9}=2.22$
The volume of A after equilibrium will be 2.22 ${{m}^{3}}$.

Note: The formulas that we have used in the question, $n=\dfrac{PV}{TR}$, and $\dfrac{{{P}_{A}}}{{{T}_{A}}}=\dfrac{{{P}_{B}}}{{{T}_{B}}}$ can only be used because the condition was mentioned that the system is an ideal system, if the system is real then we cannot use these formulas.