Question

A closed box measures 66 cm, 36 cm, and 21 cm from outside. If its walls are made of metal-sheet, \[0.5\] cm thick, then find the weight of the box, if 1 \[{\text{c}}{{\text{m}}^3}\] of metal weighs \[3.6\] gm.
A) \[17985.6\] g
B) \[15725.6\] g
C) \[13625.6\] g
D) \[15825.6\] g

Answer 1

Hint:
We are required to find the weight of the box. To do that, we will first find the external volume and the internal volume. Then, we will subtract the internal volume from external volume to find the volume of the metal sheet of the box. We will then find the weight by calculating the product of the volume of the metal sheet of the box with the weight of the unit volume of the sheet.
Formula Used: We will use the following formula \[{\text{Volume of a cuboid box}} = l \times b \times h\] unit cube, where \[l\] is the length of the cuboid, \[b\] is the breadth of the cuboid, \[h\] is the height of the cuboid.

Complete step by step solution:
We have to find the weight of a box. We are given that the closed box measures 66 cm, 36 cm, and 21 cm from outside. Its walls are made of metal-sheet, \[0.5\] cm thick. Based upon this information, let us draw the diagram of the box for a better understanding,

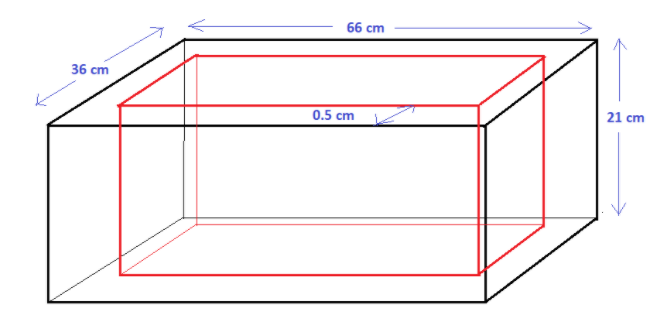
Let us first find the external volume of the box. From the given figure we can see that, the external length, \[l\] of the box, is 66 cm, the external breadth, \[b\] of the box, is 36 cm, and the external height, \[h\] of the box is 21 cm.
We will now substitute the above values in the formula for the volume of a cuboid, \[{\text{Volume of a cuboid box}} = l \times b \times h\].
On substituting the values, we get,
\[\begin{array}{l}{\text{External volume of the box}} = 66 \times 36 \times 21\\ = 49896{\text{ c}}{{\text{m}}^3}\end{array}\]

Now, we will find the internal volume of the box. To do that, we will subtract the thickness of the box from each of the length, breadth and height. Then, we will find the inner volume of the box by multiplying new length, breadth and height.
We reduce the thickness from the length here, from the two ends as can be seen in the figure. We will now find the internal length of the box, \[l'\].
\[l' = 66 - 2\left[ {{\text{thickness}}} \right]\]
Substituting \[{\text{thickness}} = 0.5\] in the above equation, we get
\[l' = 66 - 2\left( {0.5} \right)\]
Simplifying the expression, we get
\[\begin{array}{l}l' = 66 - 1\\ = 65{\text{ cm}}\end{array}\]
We reduce the thickness from the breadth here, from the two ends as can be seen in the figure. We will now find the internal breadth of the box, \[b'\].
\[b' = 36 - 2\left[ {{\text{thickness}}} \right]\]
Substituting \[{\text{thickness}} = 0.5\] in the above equation, we get
\[b' = 36 - 2\left( {0.5} \right)\]
Simplifying the expression, we get
\[\begin{array}{l}b' = 36 - 1\\ = 35{\text{ cm}}\end{array}\]
We reduce the thickness from the height here from the two ends as can be seen in the figure. We will now find the internal height of the box, \[h'\].
\[h' = 21 - 2\left[ {{\text{thickness}}} \right]\]
Substituting \[{\text{thickness}} = 0.5\] in the above equation, we get
\[h' = 21 - 2\left( {0.5} \right)\]
Simplifying the expression, we get
\[\begin{array}{l}h' = 21 - 1\\ = 20{\text{ cm}}\end{array}\]
Now, we will substitute \[l' = 65{\text{cm}}\], \[b' = 35{\text{cm}}\] and \[h' = 20{\text{cm}}\] in the formula for the volume of a cuboid, \[{\text{Volume of a cuboid box}} = l \times b \times h\].
\[\begin{array}{l}{\text{Internal Volume of the box}} = 65 \times 35 \times 20\\ = 45500{\text{c}}{{\text{m}}^3}\end{array}\]
Now, we will find the volume of the box.
\[\begin{array}{l}{\text{The volume of the box}} = {\text{External volume of the box}}-{\text{Internal volume of the box}}\\ = 49896 - 45500\\ = 4396{\text{ c}}{{\text{m}}^3}\end{array}\]
 Now, we are given that 1 \[{\text{c}}{{\text{m}}^3}\] of the metal sheet weighs \[3.6\] gm.
Hence, the total weight of the box will be,

\[\begin{array}{l}{\text{total weight of the box}} = {\text{Volume of the box}} \times {\text{Weight of the unit volume of metal sheet}}\\ = 4396 \times 3.6\\ = 15825.6\end{array}\]

Since our answer matches with option [D], hence, it is the correct option.

Note:
The volume of a box is defined as the space that is enclosed within the walls of the box. Whereas, the weight of the box determines how heavy or light the box is. Weight depends upon the volume of any substance. Weight is directly proportional to the volume. Here, we might make a mistake by thinking of the external volume as the actual volume of the box. This will give us wrong volume and ultimately the wrong weight. To calculate the right volume we need to consider the internal volume of the volume of the box. Then we will find the actual volume of the box by subtracting internal volume from external volume. This will give us the correct weight of the box.