Question

A circus artist is climbing a $60m$ long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is ${30^ \circ }$.

Answer 1

Hint:This question is from the topic heights and the distances. To solve this question, first of all we will draw the figure according to the given conditions. Then we will let height of the rope to be \[x\] .After that we will apply the formula of \[\sin \theta \] as $\sin \theta = \dfrac{\text{perpendicular}}{\text{hypotenuse}}$ and substitute the values in the formula. Finally, we will simplify and get the required result.

Complete step by step answer:
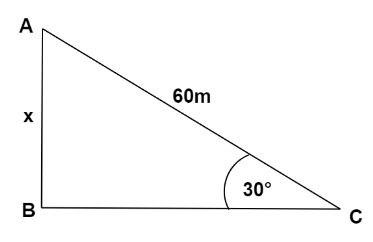
In the given question, we have length of rope $ = AB = 60\,m$. Also, the angle made by the rope with the ground level is ${30^ \circ }$. Let the height of the pole be $x$.As we know that,
$\sin \theta = \dfrac{\text{perpendicular}}{\text{hypotenuse}}$
Where $\theta = {30^ \circ }$, perpendicular $ = x$, Hypotenuse $ = 60$
Therefore, in right angled triangle $\vartriangle ABC$ ,
$\sin {30^ \circ } = \dfrac{{AB}}{{AC}}$
$\Rightarrow \dfrac{1}{2} = \dfrac{x}{{60}}$
Now on cross-multiplication, we get
$x = \dfrac{{60}}{2}$
On dividing, we get
$\therefore x = 30$

Therefore, the height of the pole is $30\,m$.

Note:The relation between the heights and distances of objects can be understood using trigonometry. Height is the measurement of an object in the vertical direction and distance is the measurement of an object from a particular point in the horizontal direction. For solving these types of questions one should know how to apply the trigonometric formulas. Basically, there are two types of angles given in the question called angle of elevation and angle of depression. You have to identify which angle is given.