Question

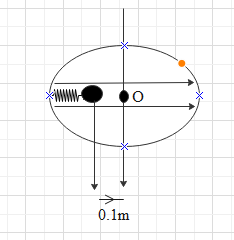
A circular turntable of radius 0.5 m has a smooth groove as shown in figure. A ball of mass 90 g is placed inside the groove along with a spring of spring constant ${{10}^{2}}N/cm$ . The ball is at a distance of 0.1 m from the centre when the turntable is at rest. On rotating the turntable with a constant angular frequency of ${{10}^{2}}{{\sec }^{-1}}$, the ball moves away from the centre by a distance nearly equal to

A. ${{10}^{-1}}m$
B. ${{10}^{-2}}m$
C. ${{10}^{-3}}m$
D. $2\times {{10}^{-1}}m$

Answer 1

Hint: Imagine the figure and try to understand the concept we will use to solve this question. The table will rote and the ball will experience a force towards outside. The ball will move but the spring will oppose this motion and at appoint restoring force of the spring will be equal to the outward centrifugal force on the ball. Equating these two terms, we can obtain the solution.

Complete step by step answer:
The radius of the circular table is $r=0.5m$
A ball with mass $m=90g=0.09kg$ is placed in the groove connecting with a spring with spring constant $k={{10}^{2}}N/cm$
Converting in the SI unit, $k={{10}^{2}}\dfrac{N}{{{10}^{-2}}m}={{10}^{4}}N/m$
The ball is at a distance 0.1 m from the centre of the table when the table is at rest.
Now, let when we rotate the table the ball will feel the centripetal force. It will move towards the side of the table till the centrifugal force is cancelled out by the opposite spring force.
Let the ball move by a distance x. so the distance of the ball from the centre of the table will be, $\left( x+0.1 \right)m$
The table is rotating with an angular velocity, $\omega ={{10}^{2}}{{s}^{-1}}$
Now the centrifugal force on the ball will be,
$\begin{align}
  & {{F}_{c}}=m{{\omega }^{2}}\left( x+0.1 \right) \\
 & {{F}_{c}}=0.09\times {{10}^{4}}\times (x+0.1) \\
\end{align}$
Restoring force of the spring on the ball will be,
$\begin{align}
  & {{F}_{s}}=kx \\
 & {{F}_{s}}={{10}^{4}}x \\
\end{align}$
Now equating both forces, we get that,
$\begin{align}
  & {{F}_{S}}={{F}_{c}} \\
 & {{10}^{4}}x=0.09\times {{10}^{4}}x+90 \\
 & 0.99\times {{10}^{4}}x=90 \\
 & x=\dfrac{90}{0.99\times {{10}^{4}}}=.9\times {{10}^{-2}} \\
 & x\approx {{10}^{-2}}m \\
\end{align}$
The correct option is (B)
Note: if we have the system as if the spring is connected to the centre of the table instead of the side, then also we would have got the same answer. This is because. The amount by which the spring opposes the compression, with the same amount of force it will also oppose the expansion of the spring.