Question

A circular piece of metal of maximum size is cut out of a square piece and then a square piece of maximum size is cut out of the circular piece. The total amount of metal wasted is
(A) \[\dfrac{1}{4}\] the area of the original square
(B) $\dfrac{1}{2}$ the area of the original square
(C) $\dfrac{1}{2}$ the area of the circular piece
(D) \[\dfrac{1}{4}\] the area of the circular piece
(E) None of these

Answer 1

Hint:The maximum diameter of the circular piece is the same as the side length of the square piece. So now we cut a square piece of maximum size from the circular piece so this square is made by joining the midpoint of the original square so we just find the area of this square and subtract it from the original square.

Complete step-by-step answer:
Let assume the side of square is $s$
$\because $ (because we have to find area of square for that we need a side)
So the maximum diameter of square is $s$
As we see in below given diagram

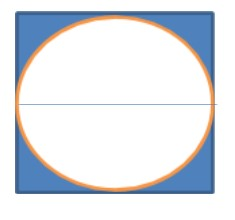
Now radius of circle $r = \dfrac{s}{2}$
Now we have to cut the square of the maximum area from the circle that we cut from the original square.
So the new square is made by joining mid-point of original square shown in diagram

So the blue part shown in this is the total amount that is wasted.
Now we find the size of new square
This can be finding with the help of Pythagorean theorem

So size of new square = $\sqrt {{{\left( {\dfrac{s}{2}} \right)}^2} + {{\left( {\dfrac{s}{2}} \right)}^2}} $
Size= $\sqrt {\left( {\dfrac{{{s^2}}}{4} + \dfrac{{{s^2}}}{4}} \right)} $
Size= $\sqrt {\dfrac{{{s^2}}}{2}} $
Size of new square is $\dfrac{s}{{\sqrt 2 }}$
Now the area of original square is = ${(side)^2}$
Area of original square is $\left( {{A_1}} \right)$= ${s^2}$
And area of square that cut from circle is $\left( {{A_2}} \right)$ = ${\left( {\dfrac{s}{{\sqrt 2 }}} \right)^2}$
${A_2} = \dfrac{{{s^2}}}{2}$
So area of wasted material $\left( A \right)$ = ${A_1} - {A_2}$
So $A = {s^2} - \dfrac{{{s^2}}}{2}$
$A = \dfrac{{{s^2}}}{2}$
So this is the $\dfrac{1}{2}$ of the original square.

So, the correct answer is “Option B”.

Note:Area of a square made by joining all the midpoint of a square is $\dfrac{1}{2}$ of the original square. In this question waste material is the all remaining part that we cut to make smallest square of maximum area from original square.